Question

【题目】定义在上的函数满足：对任意的实数，存在非零常数，都有成立.

（1）若函数，求实数和的值；

（2）当时，若， ，求函数在闭区间上的值域；

（3）设函数的值域为，证明：函数为周期函数.

Answer 1

【答案】(1) (2) (3)见解析

【解析】试题分析：（1）由得， 对恒成立，则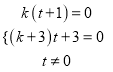，从而可得结果；（2）先根据， ，求出函数在， ， 上的解析式，从而可求得在对应区间上函数值的范围，综合可得函数在闭区间上的值域；（3）由函数的值域为得， 的取值集合也为，当时， ，则，即. 由得，则函数是以为周期的函数，同理可得当时，函数是以为周期的函数.

试题解析：（1）由得， 对恒成立，

即对恒成立，则，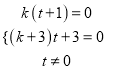

即.

（2）当时， ，

当时，即，

由得，则，

当时，即，

由得，则，

当时，即，

由得，

综上得函数在闭区间上的值域为.

（3）（证法一）由函数的值域为得， 的取值集合也为，

当时， ，则，即.

由得，

则函数是以为周期的函数.

当时， ，则，即.

即，则函数是以为周期的函数.

故满足条件的函数为周期函数.

（证法二）由函数的值域为得，必存在，使得，

当时，对，有，

对，有，则不可能；

当时，即， ，

由的值域为得，必存在，使得，

仿上证法同样得也不可能，则必有 ，以下同证法一.