题目内容
19.圆台的上、下底面半径分别为5cm、10cm,母线长AB=20cm,从圆台母线AB的中点M拉一条绳子绕圆台侧面转到A点(A在上底面),求:(1)绳子的最短长度;
(2)在绳子最短时,上底圆周上的点到绳子的最短距离;
(3)圆锥底面半径为r,母线长为4r,求从底面边缘一点A出发绕圆锥侧面一周再回到A的最短距离.
分析 (1)由题意需要画出圆台的侧面展开图,并还原成圆锥展开的扇形,则所求的最短距离是平面图形两点连线;
(2)根据条件求出扇形的圆心角以及半径长,在求出最短的距离;
(3)画出圆台的侧面展开图,有(1)中结论,可得圆心角θ=$\frac{π}{2}$,进而得到答案.
解答 解:(1)画出圆台的侧面展开图,
并还原成圆锥展开的扇形,且设扇形的圆心为O.
有图得:所求的最短距离是MB',
设OA=R,圆心角是θ,则由题意知,
10π=θR ①,20π=θ(20+R) ②,由①②解得,θ=$\frac{π}{2}$,R=20,
∴OM=30,OB'=40,则MB'=50cm.
故绳子最短的长度为:50cm.
(2)作OC垂直于B'M交于D,OC是顶点O到MB'的最短距离,
则DC是MB'与弧AA'的最短距离,DC=OC-OD=$\frac{OM•OB′}{MB′}$-20=4cm,
即绳子上各点与上底面圆周的最短距离是:4cm.
(3)画出圆台的侧面展开图,
∵圆锥底面半径为r,母线长为4r,
则圆心角θ=$\frac{π}{2}$,
故从底面边缘一点A出发绕圆锥侧面一周再回到A的最短距离为:4$\sqrt{2}$r.
点评 本题考查了在几何体表面的最短距离的求出,一般方法是把几何体的侧面展开后,根据题意作出最短距离即两点连线,结合条件求出,考查了转化思想.

练习册系列答案
相关题目
7.则“x=2”是“x2-3x+2=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.偶函数f(x)满足f(x+4)=f(x),且f(x)=$\left\{\begin{array}{l}{{3}^{x},1<x<2}\\{lo{g}_{3}x,0<x<1}\end{array}\right.$,设a=f(-9.3),b=f(-2.8),c=f(-7.3),则a,b,c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |
8.若直线l1:y=kx-2和直线l2:2x+y=4的交点在第一象限,则直线l1的倾斜角的范围是( )
| A. | ($\frac{π}{6}$,$\frac{π}{4}$) | B. | ($\frac{π}{4}$,$\frac{π}{2}$) | C. | ($\frac{π}{4}$,$\frac{π}{2}$] | D. | ($\frac{π}{4}$,$\frac{π}{3}$] |
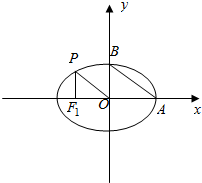 已知A、B分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点、上顶点,过左焦点F1作PF1⊥x轴,与椭圆在x轴上方的交点为P,且OP∥AB.
已知A、B分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点、上顶点,过左焦点F1作PF1⊥x轴,与椭圆在x轴上方的交点为P,且OP∥AB.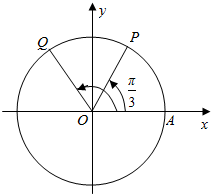 如图,∠AOP=$\frac{π}{3}$,Q点与P点关于y轴对称,P,Q都为角的终边与单位圆的交点,求:
如图,∠AOP=$\frac{π}{3}$,Q点与P点关于y轴对称,P,Q都为角的终边与单位圆的交点,求: