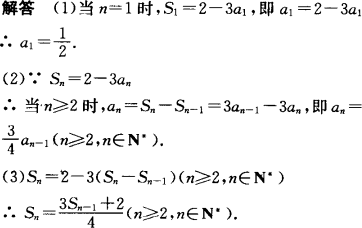题目内容
已知数列{an}的通项公式an与前n项和公式Sn之间满足关系Sn=2-3an.
(1)求a1;
(2)求an与an-1(n≥2,n∈N*)的递推关系;
(3)求Sn与Sn-1(n≥2,n∈N*)的递推关系.
答案:
解析:
解析:
|
思路与技巧:本例显然是利用an与Sn的关系来求解.通过已知条件得到an与an-1(n≥2,n∈N*)的递推关系或者Sn与Sn-1(n≥2,n∈N*)的递推关系,都可以转化为等比数列,进而求出{an}的通项公式. 评析:关系式an=Sn-Sn-1(n≥2,n∈N*)对一切数列都适用.运用关系式an=Sn-Sn-1时千万别忘掉条件:n≥2,n∈N*. |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知数列{an}的通项为an=2n-1,Sn为数列{an}的前n项和,令bn=
,则数列{bn}的前n项和的取值范围为( )
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|