题目内容
直线 为异面直线,直线
为异面直线,直线 上有4个点,直线
上有4个点,直线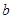 上有5个点,以这些点为顶点的三角形共有 个;
上有5个点,以这些点为顶点的三角形共有 个;
 为异面直线,直线
为异面直线,直线 上有4个点,直线
上有4个点,直线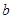 上有5个点,以这些点为顶点的三角形共有 个;
上有5个点,以这些点为顶点的三角形共有 个;70
试题分析:因为直线a上有4个点,所以,可以组成线段的条数是:3+2+1=6(条),直线a上的一个点和直线b的一条线段构成三角形的个数是:6×5=30(个),又因为,直线b上有5个点,所以,可以组成线段的条数是:4+3+2+1=10(个),直线b上的一条线段和直线a上的一个点构成三角形的个数是:10×4=40(个),共有三角形的个数:30+40=70(个),故以这些点为顶点可以画出70个三角形.
点评:运用加法原理(做一件事情,完成它有N类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,…,在第N类办法中有mn种不同的方法,那么完成这件事情共有m1+m2+…+mn种不同的方法)和乘法原理(做一件事,完成它需要分成n个步骤,做第一 步有m1种不同的方法,做第二步有m2不同的方法,…,做第n步有mn不同的方法.那么完成这件事共有 N=m1m2m3…mn 种不同的方法)即可.

练习册系列答案
相关题目
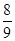
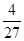
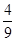
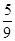
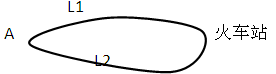
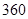 种
种 种
种 种
种 种
种