题目内容
将4本不同的书全发给3名同学,则每名同学至少有一本书的概率为( )
A.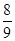 | B.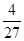 | C.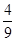 | D.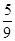 |
C
试题分析:解:4本书发给3名同学,每本书有3种分法,则4本书共有3×3×3×3=81种分发方法;要使每名同学至少有一本书,先将4本书分为2、1、1的3组,有
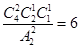 =6种分组方法,再将3组对应发给3名同学,有A33=6种情况,
=6种分组方法,再将3组对应发给3名同学,有A33=6种情况,则每名同学至少有一本书的情况有6×6=36种;故每名同学至少有一本书的概率P=
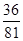 =
=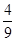 ;故答案为C.
;故答案为C.点评:本题考查排列、组合数公式的运用,关键在于运用分步的方法满足“每名同学至少有一本书”,再由分步计数原理求出其情况数目.

练习册系列答案
相关题目
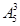
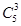
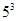
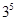
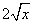 -
-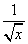 )6的二项展开式中的常数项为_____.(用数字作答)
)6的二项展开式中的常数项为_____.(用数字作答)
 ,则
,则 的值为 .
的值为 .  为异面直线,直线
为异面直线,直线 上有4个点,直线
上有4个点,直线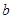 上有5个点,以这些点为顶点的三角形共有 个;
上有5个点,以这些点为顶点的三角形共有 个;