题目内容
在数列{an}中,若a1=1,且对所有n∈N+满足a1a2…an=n2,则a3+a5=( )
A.
| B.
| C.
| D.
|
由题意a1a2…an=n2,
故a1a2…an-1=(n-1)2,
两式相除得:an=
(n≥2),
所以a3=
,a5=
,
即a3+a5=
故选B.
故a1a2…an-1=(n-1)2,
两式相除得:an=
| n2 |
| (n-1)2 |
所以a3=
| 9 |
| 4 |
| 25 |
| 16 |
即a3+a5=
| 61 |
| 16 |
故选B.

练习册系列答案
相关题目
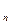 }满足a
}满足a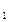 =1,a
=1,a a
a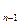 +1(n≥2),求数列{a
+1(n≥2),求数列{a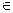 N+,都有an=n2+
N+,都有an=n2+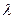 n恒成立,则实数
n恒成立,则实数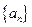 的前
的前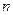 项和为
项和为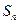 ,若
,若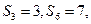 则
则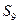 等于 。
等于 。 ,
, ,则
,则 与
与 的大小关系为 .
的大小关系为 .