题目内容
下列说法中,正确的有 .
①若点 是抛物线
是抛物线 上一点,则该点到抛物线的焦点的距离是
上一点,则该点到抛物线的焦点的距离是 ;
;
②设 、
、 为双曲线
为双曲线 的两个焦点,
的两个焦点, 为双曲线上一动点,
为双曲线上一动点, ,则
,则 的面积为
的面积为 ;
;
③设定圆 上有一动点
上有一动点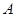 ,圆
,圆 内一定点
内一定点 ,
, 的垂直平分线与半径
的垂直平分线与半径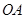 的交点为点
的交点为点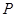 ,则
,则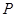 的轨迹为一椭圆;
的轨迹为一椭圆;
④设抛物线焦点到准线的距离为 ,过抛物线焦点
,过抛物线焦点 的直线交抛物线于A、B两点,则
的直线交抛物线于A、B两点,则 、
、 、
、 成等差数列.
成等差数列.
【答案】
①④
【解析】
试题分析:根据题意,由于①若点 是抛物线
是抛物线 上一点,则该点到抛物线的焦点的距离是
上一点,则该点到抛物线的焦点的距离是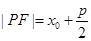 ;根据定义显然得到成立。
;根据定义显然得到成立。
②设 、
、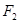 为双曲线
为双曲线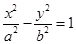 的两个焦点,
的两个焦点, 为双曲线上一动点
为双曲线上一动点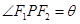 ,则
,则 的面积为
的面积为 ;结合定义和余弦定理可知面积为
;结合定义和余弦定理可知面积为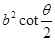 ,故错误。
,故错误。
③设定圆 上有一动点
上有一动点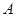 ,圆
,圆 内一定点
内一定点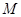 ,
,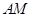 的垂直平分线与半径
的垂直平分线与半径 的交点为点
的交点为点 ,则
,则 的轨迹为一椭圆;不一定。错误
的轨迹为一椭圆;不一定。错误
④设抛物线焦点到准线的距离为 ,过抛物线焦点
,过抛物线焦点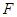 的直线交抛物线于A、B两点,则
的直线交抛物线于A、B两点,则 、
、 、
、 成等差数列.联立方程组,结合韦达定理可以证明得到
成等差数列.联立方程组,结合韦达定理可以证明得到 +
+ =
= ,进而说明结论成立,故答案为①④
,进而说明结论成立,故答案为①④
考点:圆锥曲线的性质
点评:主要是考查了圆锥曲线的方程以及性质的运用,属于中档题。

练习册系列答案
相关题目