题目内容
下列说法中,正确的有 .
①若点P(x0,y0)是抛物线y2=2px上一点,则该点到抛物线的焦点的距离是|PF|=x0+
;
②设F1、F2为双曲线
-
=1的两个焦点,P(x0,y0)为双曲线上一动点,∠F1PF2=θ,则△PF1F2的面积为b2tan
;
③设定圆O上有一动点A,圆O内一定点M,AM的垂直平分线与半径OA的交点为点P,则P的轨迹为一椭圆;
④设抛物线焦点到准线的距离为p,过抛物线焦点F的直线交抛物线于A、B两点,则
、
、
成等差数列.
①若点P(x0,y0)是抛物线y2=2px上一点,则该点到抛物线的焦点的距离是|PF|=x0+
| p |
| 2 |
②设F1、F2为双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| θ |
| 2 |
③设定圆O上有一动点A,圆O内一定点M,AM的垂直平分线与半径OA的交点为点P,则P的轨迹为一椭圆;
④设抛物线焦点到准线的距离为p,过抛物线焦点F的直线交抛物线于A、B两点,则
| 1 |
| |AF| |
| 1 |
| p |
| 1 |
| |BF| |
分析:①根据抛物线的定义进行判断.②根据双曲线的定义和性质以及三角形的面积公式进行判断.③根据椭圆的定义和性质进行判断.④根据抛物线的定义以及等差数列的定义进行判断.
解答:①抛物线的准线方程为x=-
,根据抛物线的定义可知,|PF|等于P到准线的距离即|PF|=x0+
,∴①正确.
②设|PF1|=x,|PF2|=y,(不妨设x>y),则x-y=2a,由余弦定理得|F1F2|2=x2+y2-2xycosθ,
即4c2=(x-y)2+2xy-2xycosθ,
∴4c2=4a2+xy(2-2cosθ),即xy=
,
∴△PF1F2的面积为
xysinθ=
×
×sinθ=b 2•
=b2tan
,∴②正确.
③根据垂直平分线的性质可得|PM|=|PA|,∴|PO|+|PA|=|PO|+|PM|=|OA|>|OM|,
即点P到点O和点M的距离之和等于圆的半径|OA|,且|OA|>|OM|,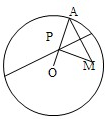
根据椭圆的定义可得点P的轨迹是以点O和点M为焦点的椭圆,∴③正确.
④设抛物线方程为y2=2px,A(x1,y1),B(x2,y2),则|AF|=x1+
,|BF|=x2+
,
设过F的直线斜率为k,若k不存在,则|AF|=|BF|=p,此时满足
、
、
成等差数列.
若k存在,则直线AB的方程为y=k(x-
),代入抛物线方程y2=2px
得k2x2-p(k2+2)x+
=0,
则x1x2=
,x1+x2=
.
∴
+
=
+
=
=
,
=
=
=
,
即
+
=
,∴
、
、
成等差数列.正确,∴④正确.
故答案为:①②③④.
| p |
| 2 |
| p |
| 2 |
②设|PF1|=x,|PF2|=y,(不妨设x>y),则x-y=2a,由余弦定理得|F1F2|2=x2+y2-2xycosθ,
即4c2=(x-y)2+2xy-2xycosθ,
∴4c2=4a2+xy(2-2cosθ),即xy=
| 4b2 |
| 2-2cosθ |
∴△PF1F2的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 4b2 |
| 2-2cosθ |
| sinθ |
| 1-cosθ |
| θ |
| 2 |
③根据垂直平分线的性质可得|PM|=|PA|,∴|PO|+|PA|=|PO|+|PM|=|OA|>|OM|,
即点P到点O和点M的距离之和等于圆的半径|OA|,且|OA|>|OM|,

根据椭圆的定义可得点P的轨迹是以点O和点M为焦点的椭圆,∴③正确.
④设抛物线方程为y2=2px,A(x1,y1),B(x2,y2),则|AF|=x1+
| p |
| 2 |
| p |
| 2 |
设过F的直线斜率为k,若k不存在,则|AF|=|BF|=p,此时满足
| 1 |
| |AF| |
| 1 |
| p |
| 1 |
| |BF| |
若k存在,则直线AB的方程为y=k(x-
| p |
| 2 |
得k2x2-p(k2+2)x+
| k2p2 |
| 4 |
则x1x2=
| p2 |
| 4 |
| k2p+2p |
| k2 |
∴
| 1 |
| |AF| |
| 1 |
| |BF| |
| 2 |
| 2x1+p |
| 2 |
| 2x2+p |
| 4(x1+x2)+4p |
| (2x1+p)(2x2+p) |
| 4×(x1+x2)+4p |
| 4x1x2+2p(x1+x2)+p2 |
=
4?(
| ||||
4?
|
| 8k2+8 |
| (4k2+4)p2 |
| 2 |
| p |
即
| 1 |
| |AF| |
| 1 |
| |BF| |
| 2 |
| p |
| 1 |
| |AF| |
| 1 |
| p |
| 1 |
| |BF| |
故答案为:①②③④.
点评:本题主要考查了圆锥曲线的定义和性质,综合性较强,难度较大,考查学生的运算能力.

练习册系列答案
相关题目