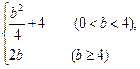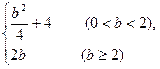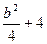题目内容

已知B（-1，1）是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，且点B到椭圆的两个焦点距离之和为4；
（1）求椭圆方程；
（2）设A为椭圆的左顶点，直线AB交y轴于点C，过C作斜率为k的直线l交椭圆于D，E两点，若
S△CBD
S△CAE
=
1
6
，求实数k的值．
（1）由题意，2a=4，∴a=2，
∵B（-1，1）是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，
∴
1
4
+
1
b2
=1
∴b2=
4
3

∴椭圆方程为
x2
4
+
3y2
4
=1
（2）由题意A（-2，0），B（-1，1），则AB的方程为y=x+2，
∴C（0，2），∴
|CB|
|CA|
=
1
2

∵
S△CBD
S△CAE
=
1
6
，∴
|CD|
|CE|
=
1
3
，
设D（x1，y1），E（x2，y2），则x2=3x1，
若CD斜率不存在，方程为x=0，D（0，
2
3
），E（0，-
2
3
），
∴
|CD|
|CE|
=
3
-1
3
+1
≠
1
3
，
若CD斜率存在，设y=kx+2，代入椭圆方程，得到（3k2+1）x2+12kx+8=0
∴x1+x2=
-12k
3k2+1
，x1x2=
8
3k2+1

∵x2=3x1，
∴k=±
2
6
3
．
练习册系列答案
相关题目
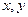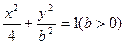若动点（）在曲线上变化，则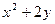的最大值为（   ）
A．B．C．D．2
已知椭圆E：
x2
a2
+
y2
3
=1（a＞
3
）的离心率e=
1
2
．直线x=t（t＞0）与曲线 E交于不同的两点M，N，以线段MN 为直径作圆 C，圆心为 C．
（1）求椭圆E的方程；
（2）若圆C与y轴相交于不同的两点A，B，求△ABC的面积的最大值．
若AB为抛物线y2=2px（p＞0）的动弦，且|AB|=a（a＞2p），则AB的中点M到y轴的最近距离是（　　）
A．
a
2
B．
p
2
C．
a+p
2
D．
a-p
2
已知椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
2
2
，并且直线y=x+b是抛物线C2：y2=4x的一条切线．
（Ⅰ）求椭圆C1的方程．
（Ⅱ）过点S(0，-
1
3
)的动直线l交椭圆C1于A、B两点，试问：在直角坐标平面上是否存在一个定点T，使得以AB为直径的圆恒过定点T？若存在求出T的坐标；若不存在，请说明理由．
如图，已知抛物线C：y2=2px和⊙M：（x-4）2+y2=1，过抛物线C上一点H（x0，y0）作两条直线与⊙M相切于A、B两点，分别交抛物线为E、F两点，圆心点M到抛物线准线的距离为
17
4
．
（1）求抛物线C的方程；
（2）当∠AHB的角平分线垂直x轴时，求直线EF的斜率．
已知定点A（2，0），它与抛物线y2=x上的动点P连线的中点M的轨迹方程为______．
如图，椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点为F（1，0），且过点（2，0）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若AB为垂直于x轴的动弦，直线l：x=4与x轴交于点N，直线AF与BN交于点M．
（ⅰ）求证：点M恒在椭圆C上；
（ⅱ）求△AMN面积的最大值．
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为e=
3
2
，且过点（
3
，
1
2
）
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线l：y=kx+m（k≠0，m＞0）与椭圆交于P，Q两点，且以PQ为对角线的菱形的一顶点为（-1，0），求：△OPQ面积的最大值及此时直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网