题目内容
函数f(x)=(x-1)0+
的定义域为( )
| 1 | ||
|
| A、(-3,1) |
| B、(-3,+∞) |
| C、(-3,1)∪(1,+∞) |
| D、(1,+∞) |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据使函数的解析式有意义的原则,结合分母不等于0,偶次被开方数不小于0,零的零次幂没有意义,可以构造关于x的不等式组,进而求解.
解答:
解:要使函数的解析式有意义,
x须满足:
解得x>-3,且x≠1
故函数的定义域为:(-3,1)∪(1,+∞),
故选:C.
x须满足:
|
解得x>-3,且x≠1
故函数的定义域为:(-3,1)∪(1,+∞),
故选:C.
点评:本题考查的知识点是函数的定义域及其求法,熟练掌握函数定义域的求解原则是解答本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
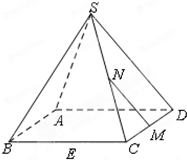 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC1;②EP∥BD;③EP∥面SBD;④EP⊥面SAC.中恒成立的为( )
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC1;②EP∥BD;③EP∥面SBD;④EP⊥面SAC.中恒成立的为( )| A、①③ | B、③④ | C、①② | D、②③④ |
已知函数f(x)=2sin(-2x+
)+1,若x∈(-
,
),则函数f(x)的值域为( )
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
A、(1-
| ||||
B、(1-
| ||||
C、[-1,1+
| ||||
| D、[-1,3] |
经过圆(x+3)2+(y-2)2=2的圆心C,且与直线x-y=0垂直的直线方程是( )
| A、x+y+1=0 |
| B、x+y-5=0 |
| C、x-y+1=0 |
| D、x-y+5=0 |
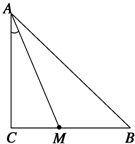 已知等腰Rt△ABC中,∠C=90°.
已知等腰Rt△ABC中,∠C=90°.