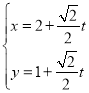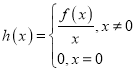题目内容
【题目】设函数![]() 是定义域R上的奇函数.
是定义域R上的奇函数.
(1)设![]() 是
是![]() 图像上的两点,求证:直线AB的斜率>0;
图像上的两点,求证:直线AB的斜率>0;
(2)求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
【答案】(1)证明见解析;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
【解析】
(1)由函数是奇函数可利用![]() 进行
进行![]() 值求解;可利用增函数的定义求证函数
值求解;可利用增函数的定义求证函数![]() 是增函数,即直线AB的斜率>0
是增函数,即直线AB的斜率>0
(2)先利用(1)的结论,设![]() ,由
,由![]() 在
在![]() 递增,可得
递增,可得![]() ,
,![]() 可化简为
可化简为![]() ,设
,设![]() ,对称轴
,对称轴![]() ,讨论对称轴与定义域的关系可进一步求得
,讨论对称轴与定义域的关系可进一步求得![]() 最值
最值
(1)由![]() ,因为函数
,因为函数![]() 是定义域R上的奇函数,所以
是定义域R上的奇函数,所以![]() ,即
,即![]() ,原表达式为
,原表达式为![]()
设![]() 是
是![]() 图像上的两点,且
图像上的两点,且![]() ,
,
则![]() ,因为
,因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,又因为
,又因为![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上为增函数,即直线AB的斜率>0
上为增函数,即直线AB的斜率>0
(2)设![]() ,由
,由![]() ,可得
,可得![]() ,由
,由![]() 在
在![]() 递增,可得
递增,可得![]() ,由
,由![]() ,即有函数
,即有函数![]()
![]() ,对称轴
,对称轴![]()
当对称轴![]() ,即
,即![]() 时,可得
时,可得![]() 时,即
时,即![]() ,最大值为2;
,最大值为2;
当对称轴![]() ,即
,即![]() 时,可得
时,可得![]() 时,即
时,即![]() 时,取得最大值
时,取得最大值![]() ;
;
综上所述,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目