题目内容
6.若0≤x≤1时,不等式1-mx≤$\frac{1}{\sqrt{1+x}}$≤1-nx恒成立,求m,n的取值范围.分析 讨论当x=0时,原不等式恒成立,当0<x≤1时,原不等式即为-m≤$\frac{\frac{1}{\sqrt{1+x}}-1}{x-0}$≤-n,$\frac{\frac{1}{\sqrt{1+x}}-1}{x-0}$的几何意义是点(0,1)与点(x,$\frac{1}{\sqrt{1+x}}$)两点的斜率,由恒成立思想即可得到所求范围.
解答 解:当x=0时,原不等式即为1≤1≤1显然成立;
当0<x≤1时,原不等式即为-m≤$\frac{\frac{1}{\sqrt{1+x}}-1}{x-0}$≤-n,
$\frac{\frac{1}{\sqrt{1+x}}-1}{x-0}$的几何意义是点(0,1)与点(x,$\frac{1}{\sqrt{1+x}}$)两点的斜率,
由于(0,1)在函数y=$\frac{1}{\sqrt{1+x}}$的图象上,且区间(0,1]为减区间.
则(0,1)与(1,$\frac{1}{\sqrt{2}}$)的斜率为$\frac{\sqrt{2}}{2}$-1,
且在(0,1]恒有斜率不大于$\frac{\sqrt{2}}{2}$-1,
即有-n≥$\frac{\sqrt{2}}{2}$-1,-m≤0,
则为m≥0,n≤1-$\frac{\sqrt{2}}{2}$.
点评 本题考查不等式恒成立问题的解法,考查两点的斜率的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
16.已知结合A={x|y=$\sqrt{x+1}$},集合B={y|y=sinx},则下列结论正确的是( )
| A. | A∩B=∅ | B. | A∪B=B | C. | A∩B=A | D. | B?A |
17.用反证法证明命题“三角形中最多只有一个内角是钝角”时,结论的否定是( )
| A. | 没有一个内角是钝角 | B. | 只有两个内角是钝角 | ||
| C. | 至少有两个内角是钝角 | D. | 三个内角都是钝角 |
11.给出下列四个结论,其中正确的是( )
| A. | 若$\frac{1}{a}>\frac{1}{b}$,则a<b | |
| B. | “a=3“是“直线l1:a2x+3y-1=0与直线l2:x-3y+2=0垂直”的充要条件 | |
| C. | 在区间[0,1]上随机取一个数x,sin$\frac{π}{2}x$的值介于0到$\frac{1}{2}$之间的概率是$\frac{1}{3}$ | |
| D. | 对于命题P:?x∈R使得x2+x+1<0,则?P:?x∈R均有x2+x+1>0 |
15.某一几何体的三视图如图所示,按照给出的尺寸(单位:cm),则这个几何体的体积为( )
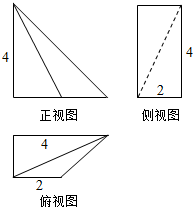

| A. | 8cm3 | B. | $\frac{40}{3}$cm3 | C. | 12cm3 | D. | $\frac{50}{3}$cm3 |