题目内容
4.求函数y=$\frac{{k}^{2}}{x}$+x(k>0)的递增区间和递减区间.分析 求函数的导数,利用导数研究函数的单调性和单调区间.
解答 解:函数的定义域为(-∞,0)∪(0,+∞),
则函数的导数为f′(x)=1-$\frac{{k}^{2}}{{x}^{2}}$,
由f′(x)>0得1-$\frac{{k}^{2}}{{x}^{2}}$>0,即$\frac{{k}^{2}}{{x}^{2}}$<1,解得x>k或x<-k,
此时函数单调递增,即函数的单调递增区间为(-∞,-k),(k,+∞),
由f′(x)<0得1-$\frac{{k}^{2}}{{x}^{2}}$<0,即$\frac{{k}^{2}}{{x}^{2}}$>1,解得-1<x<0或0<x<1,此时函数递减,
即函数的单调递减区间为(-1,0),(0,1).
点评 本题主要考查函数单调性和单调区间的求解,求函数的导数,利用导数是解决本题的关键.

练习册系列答案
相关题目
11.记f(x)=$\frac{1+x}{1-x}$,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2015(x)=( )
| A. | -$\frac{1}{x}$ | B. | x | C. | $\frac{x-1}{x+1}$ | D. | $\frac{1+x}{1-x}$ |
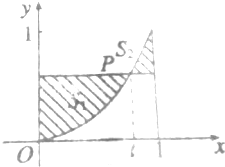 如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.
如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.