题目内容
14.设α、β、γ为不重合平面,m、n为不重合直线,下列命题正确的是③⑤①α⊥γ,β⊥γ⇒α∥β;②α⊥β,m?α,n?β⇒m⊥n;③α∥β,m?α⇒m∥β;④α∥β,m?α,n?β⇒m∥n;⑤α∥β,m∥n,m⊥α⇒n⊥β;⑥α⊥β,m⊥α⇒m∥β
分析 ①根据空间平面垂直的性质进行判断.②根据面面垂直的性质进行判断.③根据面面平行的性质进行判断.④根据面面平行的性质进行判断.⑤根据面面平行的性质进行判断.⑥根据线面平行的判定定理进行判断.
解答 解:①垂直于同一平面的两个平面不一定平行,故α⊥γ,β⊥γ⇒α∥β错误;
②α⊥β,m?α,n?β⇒m⊥n或m∥n或m,n相交或是异面直线;故②错误,
③若α∥β,m?α⇒m∥β正确;
④α∥β,m?α,n?β⇒m∥n或m,n是异面直线;故④错误,
⑤α∥β,m∥n,m⊥α,则n⊥α,⇒n⊥β成立;
⑥α⊥β,m⊥α⇒m∥β或m?β,故⑥错误,
故正确的命题是③⑤,
故答案为:③⑤.
点评 本题主要考查空间直线和平面平行或垂直的位置关系的判断,根据相应的判定定理和性质定理是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
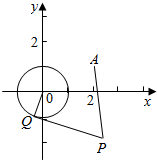 已知⊙O:x2+y2=1和定点A(2,1),⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
已知⊙O:x2+y2=1和定点A(2,1),⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.