题目内容
定义在R上的函数f(x),如果存在函数g(x)=kx+b(k,b为常数),使得f(x)≥g(x)对一切实数x都成立,则称g(x)是函数f(x)的一个“亲密函数”,现有如下的命题:
(1)对于给定的函数f(x),其“亲密函数”有可能不存在,也可能有无数个;
(2)g(x)=2x是f(x)=2x,的一个“亲密函数”;
(3)定义域与值域都是R的函数f(x),不存在“亲密函数”.
其中正确的命题是
- A.(1)
- B.(2)
- C.(1)(2)
- D.(1)(3)
A
分析:对于(1),若取f(x)=sinx,则g(x)=B(B<-1),均满足“亲密函数”函数的定义,故函数f(x)的“亲密函数”有无数个,而y=tanx,y=lgx无“亲密函数”由此可判断(1)
对于②,即x= 时,②错;
时,②错;
对于③,如取f(x)=2x+3,即可看出其不符合,故错.
抽象的背后总有具体的模型,我们可以通过具体的函数的研究,进行合理地联想.
解答:对于(1),若f(x)=sinx,则g(x)=B(B<-1),
均是它的一个亲密函数,有无数个,
再如y=tanx,y=lgx就没有亲密函数,
∴命题(1)正确、
对于(2),∵当x= 时,g(
时,g( )=3,f(
)=3,f( )=
)=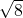 =2
=2 ,
,
∴f(x)<g(x),
∴g(x)=2x不是f(x)=2x的一个亲密函数,故错误;
对于③如f(x)=2x+3存在一个亲密函数y=2x+1,故错误;
故仅有(1)正确
故选A.
点评:本题是以抽象函数为依托,考查学生的创新能力,属于较难题,抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.
分析:对于(1),若取f(x)=sinx,则g(x)=B(B<-1),均满足“亲密函数”函数的定义,故函数f(x)的“亲密函数”有无数个,而y=tanx,y=lgx无“亲密函数”由此可判断(1)
对于②,即x=
 时,②错;
时,②错;对于③,如取f(x)=2x+3,即可看出其不符合,故错.
抽象的背后总有具体的模型,我们可以通过具体的函数的研究,进行合理地联想.
解答:对于(1),若f(x)=sinx,则g(x)=B(B<-1),
均是它的一个亲密函数,有无数个,
再如y=tanx,y=lgx就没有亲密函数,
∴命题(1)正确、
对于(2),∵当x=
 时,g(
时,g( )=3,f(
)=3,f( )=
)=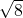 =2
=2 ,
,∴f(x)<g(x),
∴g(x)=2x不是f(x)=2x的一个亲密函数,故错误;
对于③如f(x)=2x+3存在一个亲密函数y=2x+1,故错误;
故仅有(1)正确
故选A.
点评:本题是以抽象函数为依托,考查学生的创新能力,属于较难题,抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目