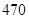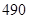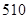题目内容
在数列{an}中,如果存在非零常数T ,使得 对于任意的非零自然数 均成立,那么就称数列
对于任意的非零自然数 均成立,那么就称数列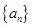 为周期数列,其中T 叫数列
为周期数列,其中T 叫数列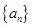 的周期。已知数列
的周期。已知数列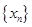 满足
满足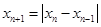 (n≥2),如果
(n≥2),如果 ,当数列
,当数列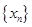 的周期最小时,该数列前2012项的和是 ( )
的周期最小时,该数列前2012项的和是 ( )
 对于任意的非零自然数 均成立,那么就称数列
对于任意的非零自然数 均成立,那么就称数列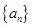 为周期数列,其中T 叫数列
为周期数列,其中T 叫数列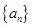 的周期。已知数列
的周期。已知数列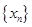 满足
满足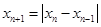 (n≥2),如果
(n≥2),如果 ,当数列
,当数列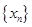 的周期最小时,该数列前2012项的和是 ( )
的周期最小时,该数列前2012项的和是 ( )| A.670 | B.671 | C.1341 | D.1340 |
D
解:题目中给出了新名词,首先要弄清题意中所说的周期数列的含义,然后利用这个定义,针对题目中的数列的周期情况分类讨论,从而将a值确定,进而将数列的前2 010项和确定。解:若其最小周期为1,则该数列是常数列,即每一项都等于1,此时a=1,
该数列的项分别为1,1,0,1,1,0,1,1,0,…,即此时该数列是以3为周期的数列;
若其最小周期为2,则有a3=a1,即|a-1|=1,a-1=1或-1,a=2或a=0,又a≠0,故a=2,
此时该数列的项依次为1,2,1,1,0,…,由此可见,此时它并不是以2为周期的数列.
综上所述,当数列{xn}的周期最小时,其最小周期是3,a=1,又2 010=3×670,
故此时该数列的前2 010项和是670×(1+1+0)=1340.
该数列的项分别为1,1,0,1,1,0,1,1,0,…,即此时该数列是以3为周期的数列;
若其最小周期为2,则有a3=a1,即|a-1|=1,a-1=1或-1,a=2或a=0,又a≠0,故a=2,
此时该数列的项依次为1,2,1,1,0,…,由此可见,此时它并不是以2为周期的数列.
综上所述,当数列{xn}的周期最小时,其最小周期是3,a=1,又2 010=3×670,
故此时该数列的前2 010项和是670×(1+1+0)=1340.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
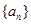 的前
的前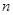 项和为
项和为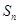 ,
,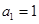 ,
,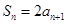 ,,则
,,则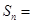
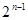
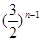
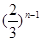
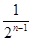
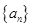 的第1项
的第1项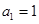 ,且
,且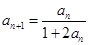
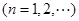 ,试归纳出这个数列的通项公式______________________________。
,试归纳出这个数列的通项公式______________________________。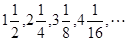 前n项的和为 ( )
前n项的和为 ( )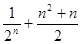
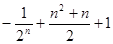
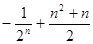
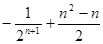
 满足
满足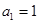 ,且
,且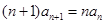 ,则数列
,则数列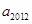 的值为( )
的值为( )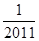
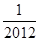
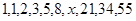 中,
中,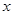 等于( )
等于( )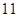
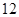
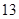
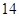
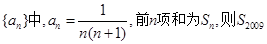 =
= 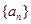 满足
满足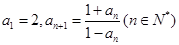 ,则
,则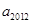 =
= 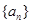 的通项
的通项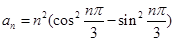 ,其前
,其前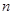 项和为
项和为 ,则
,则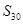 为 ( )
为 ( )