题目内容
 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,求BC的长.
B.选修4-2(矩阵与变换)
将曲线xy=1绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.
C.选修4-4(坐标系与参数方程)
求直线
|
|
D.选修4-5(不等式选讲)
已知x,y均为正数,且x>y,求证:2x+
| 1 |
| x2-2xy+y2 |
分析:A、连接OD、BD,确定△BOD是等边三角形,再在直角三角形OCD中,可得OD的长,最后根据题中圆的切线条件,依据切割线定理求得BC的长;
B、确定旋转变换矩阵,设xy=1上的任意点P'(x',y')在变换矩阵M作用下为P(x,y),确定坐标之间的关系,即可求得曲线的方程;
C、化参数方程为普通方程,求出圆心到直线的距离,即可求得截得的弦长;
D、设x=y+z(z>0),则原式=2(y+z)+
=2y+2z+
,利用基本不等式可得结论.
B、确定旋转变换矩阵,设xy=1上的任意点P'(x',y')在变换矩阵M作用下为P(x,y),确定坐标之间的关系,即可求得曲线的方程;
C、化参数方程为普通方程,求出圆心到直线的距离,即可求得截得的弦长;
D、设x=y+z(z>0),则原式=2(y+z)+
| 1 |
| z2 |
| 1 |
| z2 |
解答: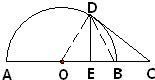 A、解:连接OD、BD,
A、解:连接OD、BD,
∵DE⊥AB,垂足为E,且E是OB的中点
∴可得等腰三角形BOD是等边三角形,
∵在直角三角形OCD中,CD=2,
∴可得OD=
,
∵CD是圆O的切线,∴由切割线定理得CD2=CB×CA,
即4=CB×(CB+
),∴BC=
;
B、解:由题意,得旋转变换矩阵M=
=
设xy=1上的任意点P'(x',y')在变换矩阵M作用下为P(x,y),则
=
∴x=
x′-
y′,y=
x′-
y′,
∵xy=1,∴
-
=1;
C、直线
(t为参数)的普通方程为x+y-2=0,圆
(α为参数)的普通方程为x2+y2=9
∴圆心到直线的距离为
=
,∴截得的弦长为2
=2
;
D、证明:设x=y+z(z>0),则原式=2(y+z)+
=2y+2z+
∵2z+
=z+z+
≥3
∴2y+2z+
≥2y+3
∴2x+
≥2y+3.
 A、解:连接OD、BD,
A、解:连接OD、BD,∵DE⊥AB,垂足为E,且E是OB的中点
∴可得等腰三角形BOD是等边三角形,
∵在直角三角形OCD中,CD=2,
∴可得OD=
2
| ||
| 3 |
∵CD是圆O的切线,∴由切割线定理得CD2=CB×CA,
即4=CB×(CB+
4
| ||
| 3 |
2
| ||
| 3 |
B、解:由题意,得旋转变换矩阵M=
|
|
设xy=1上的任意点P'(x',y')在变换矩阵M作用下为P(x,y),则
|
|
|
∴x=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵xy=1,∴
| y2 |
| 2 |
| x2 |
| 2 |
C、直线
|
|
∴圆心到直线的距离为
| 2 | ||
|
| 2 |
| 9-2 |
| 7 |
D、证明:设x=y+z(z>0),则原式=2(y+z)+
| 1 |
| z2 |
| 1 |
| z2 |
∵2z+
| 1 |
| z2 |
| 1 |
| z2 |
∴2y+2z+
| 1 |
| z2 |
∴2x+
| 1 |
| x2-2xy+y2 |
点评:本题考查选讲知识,考查几何证明选讲、旋转变换、参数方程、不等式的证明,综合性强.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
从A,B,C,D四个中选做2个,每题10分,共20分
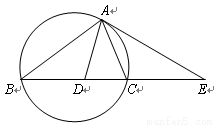
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。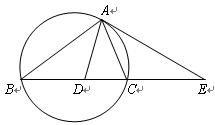 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 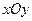 中,设椭圆 中,设椭圆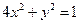 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 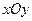 中,点 中,点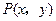 是椭圆 是椭圆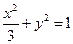 上的一个动点,求 上的一个动点,求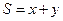 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
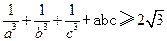 。
。 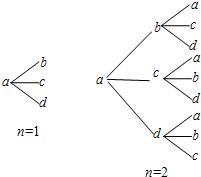 用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.
用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an. 如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,,弦CD∥AP,AD、BC相交于E点,F为CE上一点,且DE2=EF·EC.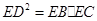 。
。
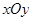 中,设椭圆
中,设椭圆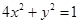 在矩阵对应的变换作用下得到曲线F,求F的方程。
在矩阵对应的变换作用下得到曲线F,求F的方程。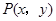 是椭圆
是椭圆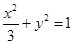 上的一个动点,求
上的一个动点,求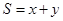 的最大值。
的最大值。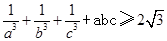 。
。