Question

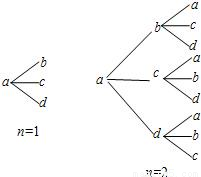
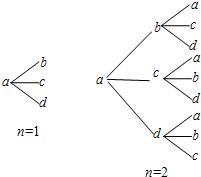用a，b，c，d四个不同字母组成一个含n+1（n∈N⁺）个字母的字符串，要求由a开始，相邻两个字母不同．例如n=1时，排出的字符串是ab，ac，ad；n=2时排出的字符串是aba，abc，abd，aca，acb，acd，ada，adb，adc，…，如图所示．记这含n+1个字母的所有字符串中，排在最后一个的字母仍是a的字符串的种数为a_n．
（1）试用数学归纳法证明：an=

3n+3(-1)n

4

(n∈N*，n≥1)；
（2）现从a，b，c，d四个字母组成的含n+1（n∈N^*，n≥2）个字母的所有字符串中随机抽取一个字符串，字符串最后一个的字母恰好是a的概率为P，求证：

2

9

≤P≤

1

3

．

Answer 1

分析：（1）根据题意，易得n=1时，等式成立，进而假设设n=k时，等式正确，再分析n=k+1时的等式与n=k的等式之间的关系，验证n=k+1时等式仍成立；综合可得证明；
（2）根据题意，易得易知P=

1

4

•

3n+3(-1)n

3n

=

1

4

[1+

3(-1)n

3n

]，分①当n为奇数（n≥3）与②当n为偶数（n≥2）两种情况，分别求得P，综合可得证明．

解答：（1）证明：
（ⅰ）当n=1时，因为a₁=0，

3+3(-1)

4

=0，所以等式正确．
（ⅱ）假设n=k时，等式正确，即ak=

3k+3(-1)k

4

(k∈N*，k≥1)，
那么，n=k+1时，因为ak+1=3k-ak=3k-

3k+3(-1)k

4

=

4•3k-3k-3(-1)k

4

=

3k+1+3(-1)k+1

4

，
这说明n=k+1时等式仍正确．
据（ⅰ），（ⅱ）可知，an=

3n+3(-1)n

4

(n∈N*，n≥1)正确；
（2）解：易知P=

1

4

•

3n+3(-1)n

3n

=

1

4

[1+

3(-1)n

3n

]，
①当n为奇数（n≥3）时，P=

1

4

(1-

3

3n

)，
因为3ⁿ≥27，所以P≥

1

4

(1-

3

27

)=

2

9

，又P=

1

4

(1-

3

3n

)＜

1

4

，所以

2

9

≤P＜

1

4

；
②当n为偶数（n≥2）时，P=

1

4

(1+

3

3n

)，
因为3ⁿ≥9，所以P≤

1

4

(1+

3

9

)=

1

3

，又P=

1

4

(1+

3

3n

)＞

1

4

，所以

1

4

＜P≤

1

3

．
综上所述，

2

9

≤P≤

1

3

．

点评：本题考查数学归纳法的运用，注意数学归纳法的步骤，2个步骤必须完整、严密，第二步尤其重要，否则将会影响解题的严密性，甚至得到错误的结论．