题目内容
已知函数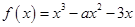
(1)若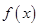 在
在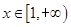 上是增函数,求实数
上是增函数,求实数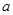 的取值范围;
的取值范围;
(2)若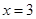 是
是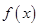 的极值点,求
的极值点,求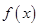 在
在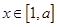 上的最小值和最大值.
上的最小值和最大值.
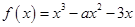
(1)若
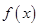 在
在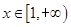 上是增函数,求实数
上是增函数,求实数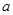 的取值范围;
的取值范围;(2)若
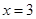 是
是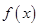 的极值点,求
的极值点,求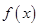 在
在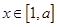 上的最小值和最大值.
上的最小值和最大值.(1) (2)f(x)max=f(1)=-6,f(x)min=-18.
(2)f(x)max=f(1)=-6,f(x)min=-18.
 (2)f(x)max=f(1)=-6,f(x)min=-18.
(2)f(x)max=f(1)=-6,f(x)min=-18.试题分析:(1)
 .
. 所以,
 时,
时, 恒成立,即
恒成立,即 恒成立 3分
恒成立 3分记
 ,
,
当
 时,t(x)是增函数,∴
时,t(x)是增函数,∴ 5分
5分故
 . 6分
. 6分(2)由题意,得
 =0,即27-6a-3=0,∴a=4, 7分
=0,即27-6a-3=0,∴a=4, 7分∴f(x)=x3-4x2-3x,
 =3x2-8x-3.
=3x2-8x-3. 令
 =0,得x1=-
=0,得x1=- ,x2=3. 8分
,x2=3. 8分当
 变化时,
变化时, 、
、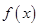 的变化情况如下表:
的变化情况如下表: | 1 | (1,3) | 3 | (3,4) | 4 |
 | | - | 0 | + | |
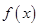 | -6 |  | 极小值 |  | -12 |
 时,
时,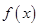 是增函数;当
是增函数;当 时,
时,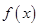 是减函数.
是减函数.于是,
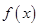 有极小值f(3)=-18; 10分
有极小值f(3)=-18; 10分而f(1)=-6,f(4)=-12,
∴f(x)max=f(1)=-6,f(x)min=-18. 12分
点评:解决的关键是利用导数的符号判定函数单调性,以及求解函数的极值和最值,属于基础题。

练习册系列答案
相关题目
 ,其中
,其中 是常数且
是常数且 .
. 时,
时, 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围;
的取值范围; 时,讨论
时,讨论 是正整数,证明:
是正整数,证明: .
. .
. 时,判断f(x)在定义域上的单调性;
时,判断f(x)在定义域上的单调性; ,求
,求 的值.
的值. .(1)求函数
.(1)求函数 的单调区间;
的单调区间; .若至少存在一个
.若至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.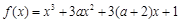 有极大值和极小值,则
有极大值和极小值,则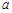 的取值范围是__ .
的取值范围是__ .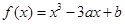 在
在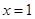 处有极小值
处有极小值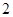 。
。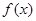 的解析式;
的解析式;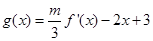 在
在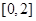 只有一个零点,求
只有一个零点,求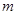 的取值范围。
的取值范围。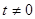 ,点P(
,点P(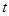 ,0)是函数
,0)是函数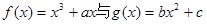 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.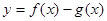 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求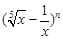 的展开式中,第4项是常数项,则
的展开式中,第4项是常数项,则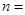
 =
=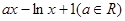 ,
,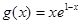 .
.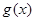 在区间
在区间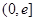 上的值域;
上的值域;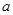 ,对任意给定的
,对任意给定的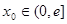 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的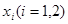 ,使得
,使得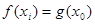 成立.若存在,求出
成立.若存在,求出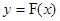 图象上任意不同的两点
图象上任意不同的两点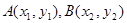 ,如果对于函数
,如果对于函数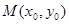 (其中
(其中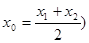 总能使得
总能使得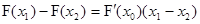 成立,则称函数具备性质“
成立,则称函数具备性质“ ”,试判断函数
”,试判断函数