题目内容
在抛物线y2=4x上求一点P,使得点P到直线y=x+3的距离最短.
解:该命题可转化为求一条平行于y=x+3的直线y=x+b与抛物线y2=4x相切,
求出切点,此时点P到直线y=x+3的距离最短,
联立方程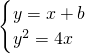
得x2+(2b-4)x+b2=0
令△=0,即(2b-4)2-4b2=0,∴b=1
故x=1,y=2,P为(1,2)
∴抛物线y2=4x上一点P(1,2),使得点P到直线y=x+3的距离最短.
分析:先设出与直线平行且与抛物线相切的直线y=x+b,与抛物线联立消去x,根据判别式等于0求得b,则切线方程可得,进而与抛物线方程联立求得切点的坐标,进而根据点到直线的距离求得答案.
点评:本题主要考查了抛物线的应用.考查了学生数形结合和转化与化归的思想.
求出切点,此时点P到直线y=x+3的距离最短,
联立方程
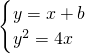
得x2+(2b-4)x+b2=0
令△=0,即(2b-4)2-4b2=0,∴b=1
故x=1,y=2,P为(1,2)
∴抛物线y2=4x上一点P(1,2),使得点P到直线y=x+3的距离最短.
分析:先设出与直线平行且与抛物线相切的直线y=x+b,与抛物线联立消去x,根据判别式等于0求得b,则切线方程可得,进而与抛物线方程联立求得切点的坐标,进而根据点到直线的距离求得答案.
点评:本题主要考查了抛物线的应用.考查了学生数形结合和转化与化归的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
点Q在抛物线y2=4x上,点P(a,0)(满足|PQ|≥|a|恒成立,则a的取值范围是( )
| A、(0,2) | B、[0,2] | C、(-∞,2] | D、(-∞,0) |