题目内容

点Q在抛物线y2=4x上，点P（a，0）（满足|PQ|≥|a|恒成立，则a的取值范围是（　　）
A、（0，2）B、[0，2]C、（-∞，2]D、（-∞，0）
分析：设出点的坐标，利用|PQ|≥|a|，可得t2+16-8a≥0，故t2≥8a-16恒成立，由此可求a的取值范围．
解答：解：设Q（
t2
4
，t），
由|PQ|≥|a|得（
t2
4
-a）2+t2≥a2，
所以t2（t2+16-8a）≥0，
即t2+16-8a≥0，
故t2≥8a-16恒成立，
所以8a-16≤0，
所以a≤2，
故a的取值范围是 （-∞，2]．
故选C．
点评：本题考查抛物线的运用，考查分离参数方法的运用，属于中档题．
练习册系列答案
相关题目
已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．
已知平面上两定点C（-1，0），D（1，0）和一定直线l：x=-4，P为该平面上一动点，作PQ⊥l，垂足为Q，且(
PQ
+2
PC
)•(
PQ
-2
PC
)=0．
（1）问点P在什么曲线上，并求出曲线的轨迹方程M；
（2）又已知点A为抛物线y2=2px（p＞0）上一点，直线DA与曲线M的交点B不在y轴的右侧，且点B不在x轴上，并满足
AB
=2
DA
，求p的最小值．
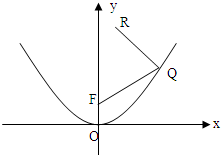如图所示，F是抛物线x2=2py（p＞0）的焦点，点R（1，4）为抛物线内一定点，点Q为抛物线上一动点，|QR|+|QF|的最小值为5．
（1）求抛物线方程；
（2）已知过点P（0，-1）的直线l与抛物线x2=2py（p＞0）相交于A（x1，y1）、B（x2，y2）两点，l1、l2分别是该抛物线在A、B两点处的切线，M、N分别是l1、l2与直线y=-1的交点．求直线l的斜率的取值范围并证明|PM|=|PN|．
（2009•武昌区模拟）已知数列{an}的各项均为正数，a1=3，点A(an，
an+1
)在抛物线y2=x+4上，则过点P（n，an）和Q（n+2，an+2）（n∈N*）的直线的一个方向向量的坐标可以是（　　）
已知定点A(3,2)在抛物线y2＝2px(p＞0)的内部, F为抛物线的焦点, 点Q在抛物线上移动, 当│AQ│+│QF│取最小值4时, p的值等于_________

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网