题目内容
已知点P在抛物线y2=4x上运动，F为抛物线的焦点，点M的坐标为（3，2），当PM+PF取最小值时点P的坐标为 ．
分析：设点P在准线上的射影为D，由抛物线的定义把问题转化为求PM+PD的最小值，同时可推断出当D，P，M三点共线时PM+PD最小，答案可得．
解答：解：设点P在准线上的射影为D，由抛物线的定义可知PF=PD，
∴要求PM+PF的最小值，即求PM+PD的最小值，
只有当D，P，M三点共线时PM+PD最小，
且最小值为3-（-1）=4
令y=2，可得x=1，
∴当PM+PF取最小值时点P的坐标为（1，2）．
故答案为：（1，2）．
∴要求PM+PF的最小值，即求PM+PD的最小值，
只有当D，P，M三点共线时PM+PD最小，
且最小值为3-（-1）=4
令y=2，可得x=1，
∴当PM+PF取最小值时点P的坐标为（1，2）．
故答案为：（1，2）．
点评：本题考查了抛物线的定义与标准方程、平面几何中求距离和的最小值等知识，正确运用抛物线的定义是关键．
练习册系列答案
一线名师权威作业本系列答案
相关题目
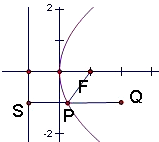已知点P在抛物线y2=4x上，那么点P到点Q（2，-1）的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为（ ）A、(
| ||
B、(
| ||
| C、（1，2） | ||
| D、（1，-2） |