题目内容
若直线y=kx+1与圆x2+y2=1相交于P、Q两点,且∠POQ=120°(其中O为原点),则k的值为( )
A.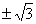 | B.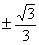 | C.±1 | D.不存在 |
A
由已知利用半径、半弦长、弦心距构成的直角三角形可得圆心O到直线y=kx+1的距离为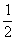 ,由点到直线的距离公式,得
,由点到直线的距离公式,得 ,解得
,解得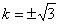 .
.
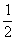 ,由点到直线的距离公式,得
,由点到直线的距离公式,得 ,解得
,解得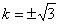 .
.
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
题目内容
A.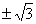 | B.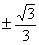 | C.±1 | D.不存在 |
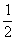 ,由点到直线的距离公式,得
,由点到直线的距离公式,得 ,解得
,解得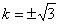 .
.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案