题目内容
2．把正整数排列成如图甲三角形数阵，然后擦去第偶数行中的奇数和第奇数行中的偶数，得到如图乙的三角形数阵，再把图乙中的数按从小到大的顺序排成一列，得到一个数列{an}，若an=2015，则n=1030．
分析 根据题意，分析图乙，可得其第k行有k个数，则前k行共有$\frac{k（k+1）}{2}$个数，第k行最后的一个数为k2，从第三行开始，以下每一行的数，从左到右都是公差为2的等差数列；进而由442＜2015＜452，可得2015出现在第45行，又由第45行第一个数为442+1=1937，由等差数列的性质，可得该行第40个数为2015，由前44行的数字数目，相加可得答案．
解答 解：分析图乙，可得①第k行有k个数，则前k行共有$\frac{k（k+1）}{2}$个数，
②第k行最后的一个数为k2，
③从第三行开始，以下每一行的数，从左到右都是公差为2的等差数列，
又由442=1936，452=2025，则442＜2015＜452，
则2015出现在第45行，
第45行第一个数为442+1=1937，这行中第$\frac{2015-1937}{2}+1$=40个数为2015，
前44行共有$\frac{44×45}{2}$=990个数，则2015为第990+40=1030个数．
故答案为：1030．
点评 本题考查归纳推理的运用，关键在于分析乙图，发现每一行的数递增规律与各行之间数字数目的变化规律，是中档题．
练习册系列答案
相关题目
13．已知直线l⊥平面α，直线m?平面β，给出下列命题：
（1）α∥β⇒l⊥m，（2）α⊥β⇒l∥m，（3）l∥m⇒α⊥β，（4）l⊥m⇒α⊥β，
其中正确的是（ ）
（1）α∥β⇒l⊥m，（2）α⊥β⇒l∥m，（3）l∥m⇒α⊥β，（4）l⊥m⇒α⊥β，
其中正确的是（ ）
| A． | （1）（2）（3） | B． | （2）（3）（4） | C． | （2）（4） | D． | （1）（3） |
7．多面体MN-ABCD的底面ABCD矩形，其正（主）视图和侧（左）视图如图，其中正（主）视图为等腰梯形，侧（左）视图为等腰三角形，则该多面体的体积为（ ）
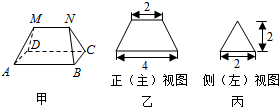
| A． | $\frac{16}{3}$ | B． | $\sqrt{6}$ | C． | $\frac{20}{3}$ | D． | 6 |
如图，梯形ABCD中，DC∥AB，AD=DC=CB=2，AB=4，矩形AEFC中，AE=$\sqrt{3}$，平面AEFC⊥平面ABCD，点G是线段EF的中点．