题目内容
14. 如图,梯形ABCD中,DC∥AB,AD=DC=CB=2,AB=4,矩形AEFC中,AE=$\sqrt{3}$,平面AEFC⊥平面ABCD,点G是线段EF的中点.
如图,梯形ABCD中,DC∥AB,AD=DC=CB=2,AB=4,矩形AEFC中,AE=$\sqrt{3}$,平面AEFC⊥平面ABCD,点G是线段EF的中点.(Ⅰ)求证:AG⊥平面BCG;
(Ⅱ)若点A,B,C,E,F都在球O的球面上,求球O的表面积.
分析 (Ⅰ)证明BC⊥AC,利用平面AEFC⊥平面ABCD,可得BC⊥平面AEFC,所以BC⊥AG,再证明AG⊥CG,即可证明AG⊥平面BCG;
(Ⅱ)由(Ⅰ)可知道CA,CB,CF两两垂直,所以可以把四棱锥B-AEFC补成以CA,CB,CF为同一顶点的一个长方体,求出外接球的直径,即可求球O的表面积.
解答  (Ⅰ)证明:在梯形ABCD中,因为AD=DC=CB=2,AB=4,
(Ⅰ)证明:在梯形ABCD中,因为AD=DC=CB=2,AB=4,
所以cos∠CBA=$\frac{\frac{4-2}{2}}{2}$=$\frac{1}{2}$,所以∠ABC=60°
由余弦定理求得AC=$\sqrt{4+16-2×2×4×\frac{1}{2}}$=2$\sqrt{3}$,
从而∠ACB=90°即BC⊥AC,
又因为平面AEFC⊥平面ABCD,所以BC⊥平面AEFC,
所以BC⊥AG,…(3分)
在矩形AEFC中,tan∠AGE=$\frac{AE}{EG}$=1,所以∠AGE=$\frac{π}{4}$,tan∠CGF=$\frac{CF}{GF}$=1,所以$∠CGF=\frac{π}{4}$,
所以∠CGF+∠AGE=$\frac{π}{2}$,即AG⊥CG,
因为BC∩CG=C
所以AG⊥平面BCG;…(6分)
(Ⅱ)解:由(Ⅰ)可知道CA,CB,CF两两垂直,所以可以把四棱锥B-AEFC补成以CA,CB,CF为同一顶点的一个长方体,…(8分)
其外接球的直径2R=$\sqrt{12+4+3}$=$\sqrt{19}$,
所以球O的表面积是S=4π•$(\frac{\sqrt{19}}{2})^{2}$=19π.…(12分)
点评 本题考查线面垂直,考查球O的表面积,正确运用线面垂直的判定,求出外接球的直径是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4. 如图,已知P是矩形ABCD所在平面外一点,PA⊥平面ABCD,E、F分别是AB,PC的中点.若∠PDA=45°,则EF与平面ABCD所成角的大小是( )
如图,已知P是矩形ABCD所在平面外一点,PA⊥平面ABCD,E、F分别是AB,PC的中点.若∠PDA=45°,则EF与平面ABCD所成角的大小是( )
 如图,已知P是矩形ABCD所在平面外一点,PA⊥平面ABCD,E、F分别是AB,PC的中点.若∠PDA=45°,则EF与平面ABCD所成角的大小是( )
如图,已知P是矩形ABCD所在平面外一点,PA⊥平面ABCD,E、F分别是AB,PC的中点.若∠PDA=45°,则EF与平面ABCD所成角的大小是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
2.把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列{an},若an=2015,则n=1030.


19. 已知抛物线C:y2=4x上一点P,若以P为圆心,|PO|为半径作圆与抛物线的准线l交于不同的两点M、N,设准线l与x轴的交点为A,则$\frac{1}{|AM|}$+$\frac{1}{|AN|}$的取值范围是
已知抛物线C:y2=4x上一点P,若以P为圆心,|PO|为半径作圆与抛物线的准线l交于不同的两点M、N,设准线l与x轴的交点为A,则$\frac{1}{|AM|}$+$\frac{1}{|AN|}$的取值范围是
( )
 已知抛物线C:y2=4x上一点P,若以P为圆心,|PO|为半径作圆与抛物线的准线l交于不同的两点M、N,设准线l与x轴的交点为A,则$\frac{1}{|AM|}$+$\frac{1}{|AN|}$的取值范围是
已知抛物线C:y2=4x上一点P,若以P为圆心,|PO|为半径作圆与抛物线的准线l交于不同的两点M、N,设准线l与x轴的交点为A,则$\frac{1}{|AM|}$+$\frac{1}{|AN|}$的取值范围是( )
| A. | (0,$\sqrt{2}$) | B. | ($\sqrt{2}$,+∞) | C. | (0,2$\sqrt{2}$) | D. | (2$\sqrt{2}$,+∞) |
 如图是某校限时12min跑体能达标测试中计算每一位参加测试的学生所跑路程S(单位:m)及时间t(单位:min)的流程图,每跑完一圈(400m),计一次路程,12min内达标或超过12min则停止计程.某同学成功通过该项测试,则该同学所跑路程至少为2000m.
如图是某校限时12min跑体能达标测试中计算每一位参加测试的学生所跑路程S(单位:m)及时间t(单位:min)的流程图,每跑完一圈(400m),计一次路程,12min内达标或超过12min则停止计程.某同学成功通过该项测试,则该同学所跑路程至少为2000m. 如图,点C是以A,B为直径的圆O上不与A,B重合的一个动点,S是圆O所在平面外一点,且总有SC⊥平面ABC,M是SB的中点,AB=SC=2.
如图,点C是以A,B为直径的圆O上不与A,B重合的一个动点,S是圆O所在平面外一点,且总有SC⊥平面ABC,M是SB的中点,AB=SC=2.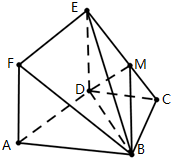 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=$\frac{1}{2}$AB=1,点M在线段EC上.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=$\frac{1}{2}$AB=1,点M在线段EC上.