题目内容
7．多面体MN-ABCD的底面ABCD矩形，其正（主）视图和侧（左）视图如图，其中正（主）视图为等腰梯形，侧（左）视图为等腰三角形，则该多面体的体积为（ ）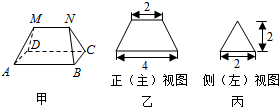
| A． | $\frac{16}{3}$ | B． | $\sqrt{6}$ | C． | $\frac{20}{3}$ | D． | 6 |
分析 利用三视图的数据，把几何体分割为2个三棱锥1个三棱柱，求解体积即可．
解答 
解：用割补法可把几何体分割成三部分，如图：棱锥的高为2，底面边长为4，2的矩形，棱柱的高为2．
可得$V=\frac{2×2}{2}×2+（{\frac{1}{3}×1×2×2}）×2=\frac{20}{3}$，
故选：C．
点评 本题考查三视图复原几何体的体积的求法，考查计算能力．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
2．把正整数排列成如图甲三角形数阵，然后擦去第偶数行中的奇数和第奇数行中的偶数，得到如图乙的三角形数阵，再把图乙中的数按从小到大的顺序排成一列，得到一个数列{an}，若an=2015，则n=1030．
19．
已知抛物线C：y2=4x上一点P，若以P为圆心，|PO|为半径作圆与抛物线的准线l交于不同的两点M、N，设准线l与x轴的交点为A，则$\frac{1}{|AM|}$+$\frac{1}{|AN|}$的取值范围是
（ ）
已知抛物线C：y2=4x上一点P，若以P为圆心，|PO|为半径作圆与抛物线的准线l交于不同的两点M、N，设准线l与x轴的交点为A，则$\frac{1}{|AM|}$+$\frac{1}{|AN|}$的取值范围是（ ）
| A． | （0，$\sqrt{2}$） | B． | （$\sqrt{2}$，+∞） | C． | （0，2$\sqrt{2}$） | D． | （2$\sqrt{2}$，+∞） |
16．sin240°的值为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |