��Ŀ����
����Ŀ��ƹ�����������涨��һ�ֱ�����˫���ȷ���10ƽǰ��һ����������2�κԷ�����������2�Σ������ֻ�.ÿ�η���ʤ����1�֣�������0��.���ڼס��ҵı����У�ÿ�η�����1�ֵĸ���Ϊ0.6�����η����ʤ����������.�ס��ҵ�һ�ֱ����У����ȷ���.
��1����ʼ��4�η���ʱ���ס��ҵıȷ�Ϊ1��2�ĸ��ʣ�
��2��![]() ��ʾ��ʼ��4�η���ʱ�ҵĵ÷֣���
��ʾ��ʼ��4�η���ʱ�ҵĵ÷֣��� ![]() ������.
������.
���𰸡�
��1���⣺�� ![]() ��ʾ�¼�����1�κ͵ڶ��������η�����
��ʾ�¼�����1�κ͵ڶ��������η����� ![]() �֣�
�֣� ![]() ��
��
![]() ��ʾ�¼�����3�η���1�֣�
��ʾ�¼�����3�η���1�֣�
![]() ��ʾ�¼�����ʼ��4�η���ʱ�����ҵıȷ�Ϊ1��2.
��ʾ�¼�����ʼ��4�η���ʱ�����ҵıȷ�Ϊ1��2.
![]() .
.
![]()
![]()
��2���⣺ ![]() .
.
![]() �Ŀ���ȡֵΪ0��1��2��3.
�Ŀ���ȡֵΪ0��1��2��3.
![]() .
.
![]() .
.
![]() .
.
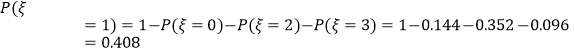 .����
.���� ![]() ��
��
![]()
![]()
��������(1)�������֪�ס��ҵıȷ�Ϊ1��2������ܵ���������֣����ݻ����¼�������¼��ĸ������ɵõ�����ʡ�(2)��������õ��� �Ŀ���ȡֵ���ö����¼��ĸ��ʹ�ʽ������Ȼ�������ѧ�����Ĺ�ʽ�����ֵ���ɡ�

��ϰ��ϵ�д�
 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
�����Ŀ