题目内容
设函数 .
.
(1)求f(x)的单调区间和极值;
(2)关于 的方程f(x)=a在区间
的方程f(x)=a在区间 上有三个根,求a的取值范围.
上有三个根,求a的取值范围.
(1) f(x)的单调增区间为 ,
, ;单调减区间为
;单调减区间为 ;当
;当 时f(x)有极大值
时f(x)有极大值 ,当x=2时, f(x)有极小值-8.
,当x=2时, f(x)有极小值-8.
(2) 
解析试题分析:(1)首先求出函数的导数,然后根据导数与单调区间的关系确定函数的单调区间,根据函数单调性即可求得函数极值;
(2)关于 的方程f(x)=a在区间
的方程f(x)=a在区间 上有三个根,即函数y=a与y=f(x)的图象在区间
上有三个根,即函数y=a与y=f(x)的图象在区间 上有三个交点,只需要函数y=" f(x)" 和函数y="a" 的图像有两个交点.根据函数单调性变化情况,可求得实数a的值.
上有三个交点,只需要函数y=" f(x)" 和函数y="a" 的图像有两个交点.根据函数单调性变化情况,可求得实数a的值.
(1) 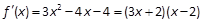 ,由
,由 得
得 (2分)
(2分)
由上表得, f(x)的单调增区间为x 


2 
f’(x) + 0 - 0 + f(x) ↗ 极大值 
↘ 极小值 
↗  ,
, ;单调减区间为
;单调减区间为 ;
;
当 时f(x)有极大值
时f(x)有极大值 ,当x=2时, f(x)有极小值-8. (6分)
,当x=2时, f(x)有极小值-8. (6分)
(2)由题知,只需要函数y=" f(x)" 和函数y="a" 的图像有两个交点. (7分)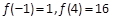 ,所以
,所以
由(1)知f(x)在,当 上单调递减,
上单调递减,  上单调递增,在
上单调递增,在 在上单调递减. (10分)
在上单调递减. (10分)
∴当 时, y=" f(x)" 和y="a" 的图像有两个交点.即方程f(x)=a在区间
时, y=" f(x)" 和y="a" 的图像有两个交点.即方程f(x)=a在区间 上有三个根. (12分)
上有三个根. (12分)
考点:函数的单调区间和极值;函数图像的交点与方程的根的对应关系.

练习册系列答案
相关题目

 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数). 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值. 为实数,
为实数,
 ;
; ,求
,求 在[-2,2] 上的最大值和最小值.
在[-2,2] 上的最大值和最小值. .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 时
时 ,求a的取值范围.
,求a的取值范围. 是函数
是函数 的一个极值点,其中
的一个极值点,其中 .
. 与
与 的关系式;
的关系式; 的单调区间;
的单调区间; 时,函数
时,函数 ,求
,求 为常数,且
为常数,且 ,函数
,函数 ,
,
 是自然对数的底数).
是自然对数的底数). 的值;
的值; 的单调区间;
的单调区间; 时,是否同时存在实数
时,是否同时存在实数 和
和 (
( ),使得对每一个
),使得对每一个 ,直线
,直线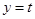 与曲线
与曲线
 都有公共点?若存在,求出最小的实数
都有公共点?若存在,求出最小的实数 ,( a为常数,e为自然对数的底).
,( a为常数,e为自然对数的底).

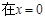 时取得极小值,试确定a的取值范围;
时取得极小值,试确定a的取值范围; 的极大值构成的函数
的极大值构成的函数 ,将a换元为x,试判断
,将a换元为x,试判断 是否能与
是否能与 (m为确定的常数)相切,并说明理由.
(m为确定的常数)相切,并说明理由. ,曲线
,曲线 在点
在点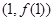 处的切线方程为
处的切线方程为


 ,其中
,其中 .
. 在点
在点 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式; ,不等式
,不等式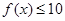 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.