题目内容
5.已知向量$\overrightarrow{a}$=($\frac{1}{2}$sin2x,cos2x-$\frac{1}{2}$),$\overrightarrow{b}$=(sinφ,cosφ),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$(0<φ<π),其图象过点($\frac{π}{8}$,$\frac{1}{2}$)(1)求φ的值和f(x)的图象的对称中心;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[0,$\frac{π}{4}$]上的最大值和最小值.
分析 (1I)首先,利用降幂公式、辅助角公式化简函数解析式,然后,根据三角函数的对称中心进行求解即可;
(2)借助于三角函数的图象变换,得到函数g(x)的解析式,然后,确定其最大值和最小值即可.
解答 解:(1)∵f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$
=$\frac{1}{2}$sin2xsinφ+cosφ(cos2x-$\frac{1}{2}$)
=$\frac{1}{2}$sin2xsinφ+$\frac{1}{2}$cosφcos2x
=$\frac{1}{2}$cos(2x-φ),
∴f(x)=$\frac{1}{2}$cos(2x-φ),
∵其图象过点($\frac{π}{8}$,$\frac{1}{2}$),
∴cos($\frac{π}{4}$-φ)=1,
∵0<φ<π,
∴φ=$\frac{π}{4}$,
∴f(x)=$\frac{1}{2}$cos(2x-$\frac{π}{4}$),
令2x-$\frac{π}{4}$=$\frac{π}{2}$+kπ,
∴2x=$\frac{3π}{4}$+kπ,
∴x=$\frac{3π}{8}$+$\frac{kπ}{2}$,k∈Z,
∴对称中心($\frac{3π}{8}$+$\frac{kπ}{2}$,0),(k∈Z),
(2)结合图象变换,得
g(x)=2cos(4x-$\frac{π}{4}$),
∵0≤x≤$\frac{π}{2}$,
0≤4x≤2π,
∴-$\frac{π}{4}$≤4x-$\frac{π}{4}$≤$\frac{7π}{4}$,
∴-2≤2cos(4x-$\frac{π}{4}$)≤2,
∴最大值2和最小值-2.
点评 本题属于综合题,综合考查了三角公式、二倍角公式、辅助角公式、三角函数的图象与性质等知识,属于中档题.

 字词句段篇系列答案
字词句段篇系列答案| A. | a2>b2 | B. | $\frac{b}{a}$<1 | C. | lg(a-b)>lg$\frac{1}{a-b}$ | D. | 4-a<4-b |
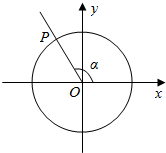 如图,已知角α的终边在第二象限,且与单位圆交于点P(m,$\frac{\sqrt{15}}{4}$).
如图,已知角α的终边在第二象限,且与单位圆交于点P(m,$\frac{\sqrt{15}}{4}$).