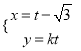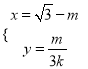题目内容
【题目】已知函数![]() 的图象过点
的图象过点![]() ,图象与P点最近的一个最高点坐标为
,图象与P点最近的一个最高点坐标为![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)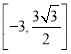 ;(3)
;(3)![]()
【解析】
(1)由最值求解A,由已知特殊点可求周期,进而可求ω,然后由点的坐标代入可求φ,即可求解函数解析式,进而求得单调增区间;
(2)由x的范围,结合正弦函数的性质可求函数的值域;
(3)结合已知及诱导公式及正弦函数的对称性可求.
(1)由题意可得,A=3,![]() ,
,
所以T=π,ω=2,f(x)=3sin(2x+φ),
又![]() ,且
,且![]() ,
,
故![]() ,解得
,解得![]() ,
,
令![]() ,
,
解得![]() ,
,
所以增区间为![]() ;
;
(2)由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴![]() 即函数的值域
即函数的值域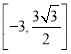 ;
;
(3)由![]() 可得
可得![]() ,
,
所以![]() ,
,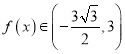 ,
,
因为方程f(x)=1在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,
不妨设![]() ,
,
且![]() ,
,
则![]()
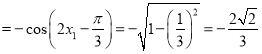 .
.

练习册系列答案
相关题目
【题目】某班甲、乙两名同学参加l00米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
甲 | 11.6 | 12.2 | 13.2 | 13.9 | 14.0 | 11.5 | 13.1 | 14.5 | 11.7 | 14.3 |
乙 | 12.3 | 13.3 | 14.3 | 11.7 | 12.0 | 12.8 | 13.2 | 13.8 | 14.1 | 12.5 |
(I)请作出样本数据的茎叶图;如果从甲、乙两名同学中选一名参加学校的100米比赛,从成绩的稳定性方面考虑,选派谁参加比赛更好,并说明理由(不用计算,可通过统计图直接回答结论).
(Ⅱ)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率.
(Ⅲ)经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在![]() 之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于
之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于![]() 秒的概率.
秒的概率.