Question

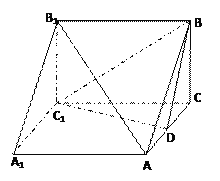
【题目】如图，三棱柱中，⊥面，，

，D为AC的中点.

（Ⅰ）求证：面BD；

（Ⅱ）求二面角的余弦值；

Answer 1

【答案】（Ⅰ）见解析（Ⅱ）

【解析】

（Ⅰ）连接B1C，与BC1相交于O，连接OD．根据三角形的中位线定理判定线面平行。

（Ⅱ）建立空间直角坐标系，求得面BDC1的一个法向量和面ABC的一个法向量，利用法向量求面面夹角，并判断二面角的大小。

（I）证明：连接B1C，与BC1相交于O，连接OD．

∵BCC1B1是矩形，∴O是B1C的中点．

又D是AC的中点，∴OD//AB1． ∵AB1面BDC1，OD面BDC1，∴AB1//面BDC1．

（II）解：如图，建立空间直角坐标系，

则C1（0，0，0），B（0，3，2），

C（0，3，0），A（2，3，0）D（1，3，0），

，，

设是面BDC1的一个法向量，则

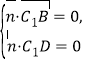即，取.

易知是面ABC的一个法向量.

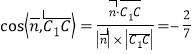. ∴二面角C1—BD—C的余弦值为.