题目内容
已知定义域为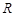 的函数
的函数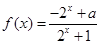 是奇函数.
是奇函数.
(Ⅰ)求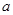 值;
值;
(Ⅱ)判断并证明该函数在定义域R上的单调性;
(Ⅲ)设关于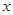 的函数
的函数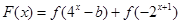 有零点,求实数
有零点,求实数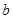 的取值范围.
的取值范围.
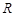 的函数
的函数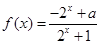 是奇函数.
是奇函数.(Ⅰ)求
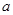 值;
值;(Ⅱ)判断并证明该函数在定义域R上的单调性;
(Ⅲ)设关于
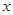 的函数
的函数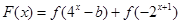 有零点,求实数
有零点,求实数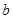 的取值范围.
的取值范围.(Ⅰ)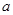 =1.(Ⅱ)f(x)在R上为减函数..(Ⅲ)
=1.(Ⅱ)f(x)在R上为减函数..(Ⅲ)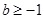 .
.
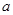 =1.(Ⅱ)f(x)在R上为减函数..(Ⅲ)
=1.(Ⅱ)f(x)在R上为减函数..(Ⅲ)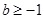 .
.试题分析:(Ⅰ)根据奇函数的定义域为R可求出
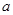 的值.(Ⅱ)已知函数式化简后计算会简单些,通过单调性的定义证明函数在R上是递减的.(Ⅲ)通过第二步的单调性可得两个变量要相等,求出b的范围.本题包含了函数的奇偶性的知识,单调性的知识,同时对单调性做了一个应用.综合性较强难度不算大.第三步的范围有一定的难度,最后转化为根的存在性所以b应该大于或等于
的值.(Ⅱ)已知函数式化简后计算会简单些,通过单调性的定义证明函数在R上是递减的.(Ⅲ)通过第二步的单调性可得两个变量要相等,求出b的范围.本题包含了函数的奇偶性的知识,单调性的知识,同时对单调性做了一个应用.综合性较强难度不算大.第三步的范围有一定的难度,最后转化为根的存在性所以b应该大于或等于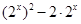 的最小值,这个解题思想要理解把握.
的最小值,这个解题思想要理解把握.试题解析:(Ⅰ)因为f(x)的定义域为R且为奇函数,所以f(0)=0,解得
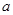 =1,经检验符合.
=1,经检验符合.(Ⅱ)
 ,f(x)在R上为减函数下:设在R上为减函数.
,f(x)在R上为减函数下:设在R上为减函数. 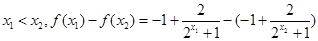
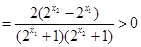 .所以f(x)在R上为减函数.
.所以f(x)在R上为减函数.(Ⅲ)因为F(x)=0,所以
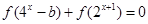 ,
,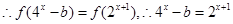 有解.所以b=
有解.所以b=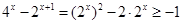

练习册系列答案
相关题目
 ,
, 且
且 。
。 的值;
的值; 在区间
在区间 上的单调性.
上的单调性.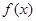 满足
满足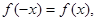 当
当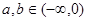 时,总有
时,总有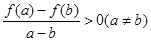 .若
.若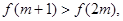 则实数
则实数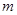 的取值范围是 .
的取值范围是 .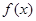 是定义在R上的奇函数且单调递减,若
是定义在R上的奇函数且单调递减,若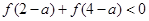 ,则
,则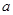 的取值范围是( )
的取值范围是( )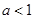
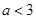
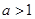
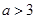
 的图象向右平移
的图象向右平移 个单位后关于
个单位后关于 对称,当
对称,当 时,
时, <0恒成立,设
<0恒成立,设 ,
, ,
, ,则
,则 的大小关系为( )
的大小关系为( )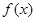 中,满足“对任意
中,满足“对任意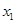 ,
,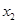
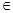 (0,
(0,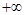 ),当
),当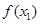 >
>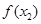 的是 ( )
的是 ( )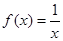
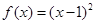
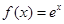
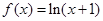
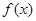 是定义在
是定义在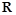 上的奇函数,且当
上的奇函数,且当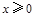 时,
时,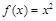 ,若对任意
,若对任意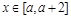 ,不等式
,不等式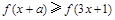 恒成立,则实数
恒成立,则实数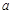 的取值范围是 .
的取值范围是 .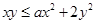 对于
对于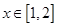 ,
,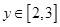 恒成立,则实数
恒成立,则实数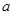 的取值范围是___________.
的取值范围是___________.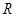 上的函数
上的函数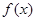 是最小正周期为
是最小正周期为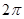 的偶函数,
的偶函数,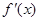 是
是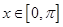 时,
时,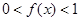 ;当
;当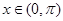 且
且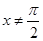 时 ,
时 ,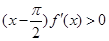 ,则函数
,则函数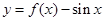 在
在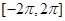 上的零点个数为( )
上的零点个数为( )