题目内容
已知二次函数
(1)若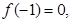 试判断函数
试判断函数 零点个数;
零点个数;
(2)若对任意的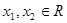 ,且
,且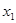 <
<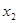 ,
,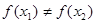 (
(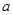 >0),试证明:
>0),试证明: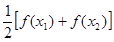 >
>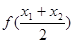 成立。
成立。
(3)是否存在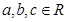 ,使
,使 同时满足以下条件:①对任意
同时满足以下条件:①对任意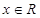 ,
, ,且
,且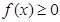 ②对任意的
②对任意的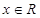 ,都有
,都有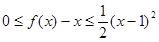 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(1) 零点为1个或2个;(2)见解析;(3)  。
。
解析试题分析:(1)∵f(-1)=0,∴a-b+c=0即b=a+c,故△=b2-4ac=(a+c)2-4ac=(a-c)2,
当a=c时,△=0,函数f(x)有一个零点;当a≠c时,△>0,函数f(x)有两个零点.
(2)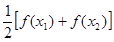 -
-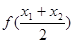 =
=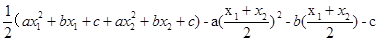
=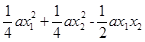 =
=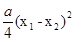
因为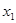 <
<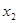 ,
,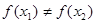 (
(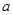 >0)所以
>0)所以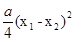 >0,即
>0,即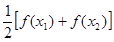 -
-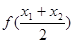 >0,
>0,
所以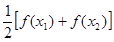 >
>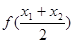 成立。
成立。
(3)假设存在a,b,c满足题设,由条件①知抛物线的对称轴为x=-1且f(x)min=0;?∴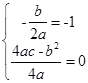 即
即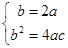 ,所以a=c,在条件②中令x=1,有0≤f(1)-1≤0,?∴f(1)=1,?即a+b+c=1,由
,所以a=c,在条件②中令x=1,有0≤f(1)-1≤0,?∴f(1)=1,?即a+b+c=1,由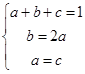 得
得 ,所以存在
,所以存在 使f(x)同时满足条件①②。
使f(x)同时满足条件①②。
考点:本题考查函数的零点与方程根的关系。
点评:本题考查函数零点个数与方程根的个数问题,以及存在性问题的处理方式,属于较难的题目.主要分析思路(1)通过对二次函数对应方程的判别式进行分析判断方程根的个数,从而得到零点的个数;(2)存在性问题的一般处理方法就是假设存在,然后根据题设条件求得参数的值.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
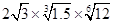 ; (2)已知
; (2)已知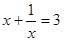 求
求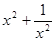 的值
的值 定义在
定义在 上,对于任意实数
上,对于任意实数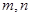 ,恒有
,恒有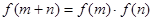 ,且当
,且当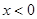 时,
时,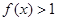
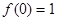 ,且当
,且当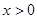 时,
时, 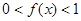
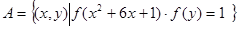 ,
,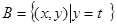 ,且
,且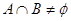 ,
,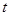 的取值范围.
的取值范围.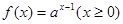 的图象经过点
的图象经过点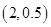 ,其中
,其中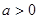 且
且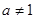 。
。 的值;
的值; ;
;
 百件时,若
百件时,若 ,则销售所得的收入为
,则销售所得的收入为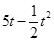 万元:若
万元:若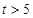 ,则销售收入为
,则销售收入为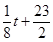 万元.
万元.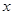 百件
百件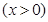 ,请把该公司生产并销售这种产品所得的年利润
,请把该公司生产并销售这种产品所得的年利润 表示为当年生产量
表示为当年生产量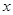 万元满足
万元满足 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本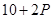 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为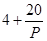 元/万件.
元/万件.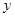 万元表示为促销费用
万元表示为促销费用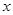 万元满足
万元满足 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本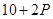 万元(不含促销费用),每件产品的销售价格定为
万元(不含促销费用),每件产品的销售价格定为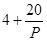 元.
元. 万元表示为促销费用
万元表示为促销费用