题目内容
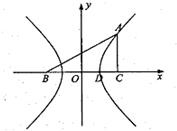 直角三角形ABC中,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
直角三角形ABC中,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.(1)求双曲线E的方程;
(2)若一过点P(3,0)的直线l与双曲线E相交于不同于双曲线顶点的两点M、N,且
| MP |
| PN |
| BC |
| GM |
| GN |
分析:(1)设出双曲线的方程,则可表示出B,C,D坐标,根据BD=3DC求得a和c的关系,进而利用双曲线的定义以及三角形的周长建立方程组求得a,进而求得c和b,则双曲线的方程可得.
(2)在x轴上存在定点G使题设成立,设出直线l的方程,根据
=λ
求得x1-t=λ(x2-t),把直线方程代入椭圆方程消去y,利用韦达定理表示出x1+x2和x1x2,进而求得t,则定点G的坐标可求.
(2)在x轴上存在定点G使题设成立,设出直线l的方程,根据
| MP |
| PN |
解答:解:(1)解:设双曲线E的方程为
-
=1 (a>0,b>0),
则B(-c,0),D(a,0),C(c,0).
由BD=3DC,得c+a=3(c-a),即c=2a
∴
解之得a=1,∴c=2,b=
∴双曲线E的方程为x2-
=1.
(2)解:设在x轴上存在定点G(t,0),使
⊥(
-λ
).
当l⊥x轴时,由
=λ
,显然成立
当l与x轴不垂直时,设直线l的方程为y=k(x-3),M(x1,y1),N(x2,y2)
由
=λ
,即(3-x1,y1)=λ(x2-3,y2),即3-x1=λ(x2-3),即λ=
∵
=(4,0),
-λ
=(x1-t-λx2+λt,y1-λy2),
∴
⊥(
-λ
)?x1-t=λ(x2-t),将λ=
代入得2x1x2-(3+t)(x1+x2)+6t=0①
将y=k(x-3)代入方程为x2-
=1整理得得:(3-k2)x2-6k2x-9k2-3=0
其中k2-3≠0且△>0,即k2≠
且x1+x2=
, x1x2=
代入①,得:
+
+6t=0,化简得:t=
.
因此,在x轴上存在定点G(
,0),使
⊥(
-λ
).
| x2 |
| a2 |
| y2 |
| b2 |
则B(-c,0),D(a,0),C(c,0).
由BD=3DC,得c+a=3(c-a),即c=2a
∴
|
解之得a=1,∴c=2,b=
| 3 |
∴双曲线E的方程为x2-
| y2 |
| 3 |
(2)解:设在x轴上存在定点G(t,0),使
| BC |
| GM |
| GN |
当l⊥x轴时,由
| MP |
| PN |
当l与x轴不垂直时,设直线l的方程为y=k(x-3),M(x1,y1),N(x2,y2)
由
| MP |
| PN |
| 3-x1 |
| x2-3 |
∵
| BC |
| GM |
| GN |
∴
| BC |
| GM |
| GN |
| 3-x1 |
| x2-3 |
将y=k(x-3)代入方程为x2-
| y2 |
| 3 |
其中k2-3≠0且△>0,即k2≠
| 3 |
| -6k2 |
| 3-k2 |
| -9k2-3 |
| 3-k2 |
代入①,得:
| -18k2-6 |
| 3-k2 |
| 6(t+3)k2 |
| 3-k2 |
| 1 |
| 3 |
因此,在x轴上存在定点G(
| 1 |
| 3 |
| BC |
| GM |
| GN |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生分析问题,解决问题的能力.

练习册系列答案
相关题目
 15、(选做题)(几何证明选讲选做题)如图,直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交AC边于点D,AD=2,则∠C的大小为
15、(选做题)(几何证明选讲选做题)如图,直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交AC边于点D,AD=2,则∠C的大小为 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且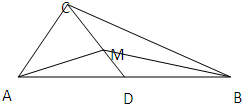 如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.
如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.