题目内容

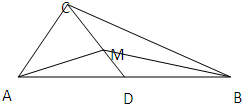精英家教网如图：直角三角形ABC中，AC⊥BC，AB=2，D是AB的中点，M是CD上的动点．
（1）若M是CD的中点，求
MA
•
MB
的值；
（2）求(
MA
+
MB
)•
MC
的最小值．
分析：（1）根据向量的线性运算，得
MA
=
MD
+
DA
且
MB
=
MD
-
DA
，因此
MA
•
MB
=
MD
2-
DA
2，再代入题中数据即可得到
MA
•
MB
的值；
（2）设MD=x，则MC=1-x，由三角形中线的性质化简得(
MA
+
MB
)•
MC
=2
MD
•
MC
=2x2-2x，接下来求二次函数y=2x2-2x在区间[0，1]上的最值，即可得到当x=
1
2
时，(
MA
+
MB
)•
MC
的最小值为-
1
2
．
解答：解：（1）∵CD是Rt△ABC的斜边AB上的中线，
∴CD=
1
2
AB=1，得MD=
1
2
CD=
1
2

∵
MA
=
MD
+
DA
，
MB
=
MD
+
DB
=
MD
-
DA
，
∴
MA
•
MB
=（
MD
+
DA
）（
MD
-
DA
）
=
MD
2-
DA
2=|
1
2
CD
|2-|
DA
|2=(
1
2
)2-12=-
3
4
．…（6分）
（2）设MD=x，则MC=1-x．其中0≤x≤1
∵MD是△MAB的中线，∴
MA
+
MB
=2
MD
，
得(
MA
+
MB
)•
MC
=2
MD
•
MC

=-2|
MD
|•|
MC
|=-2x（1-x）=2x2-2x，
∵2x2-2x=2（x-
1
2
）2-
1
2

∴当且仅当x=
1
2
时，2x2-2x的最小值为-
1
2
． …（12分）
即当x=
1
2
时，(
MA
+
MB
)•
MC
的最小值为-
1
2
．…（14分）
点评：本题给出直角三角形ABC斜边中线上的动点M，求向量数量积的最小值，着重考查了平面向量数量积的运算和二次函数在闭区间上的最值等知识点，属于中档题．
练习册系列答案
相关题目
如图，直角三角形ABC中，∠B=90°，AB=1，BC=
3
．点M，N分别在边AB和AC 上（M点和B点不重合），将△AMN沿MN翻折，△AMN变为△A′MN，使顶点A′落在边BC上（A′点和B点不重合）．设∠AMN=θ．
（1）用θ表示∠BA′M和线段AM的长度，并写出θ的取值范围；
（2）求线段AN长度的最小值．
精英家教网如图，直角三角形ABC中，∠B=90°，AB=1，BC=
3
．点M，N分别在边AB和AC上（M点和B点不重合），将△AMN沿MN翻折，△AMN变为△A'MN，使顶点A'落在边BC上（A'点和B点不重合）．设∠AMN=θ．
（1）用θ表示线段AM的长度，并写出θ的取值范围；
（2）在△AMN中，若
AN
sin∠AMN
=
MA
sin∠ANM
，求线段A'N长度的最小值．
（本题为选做题，请在下列三题中任选一题作答）
A（《几何证明选讲》选做题）．如图：直角三角形ABC中，∠B=90°，AB=4，以BC为直径的圆交边AC于点D，AD=2，则∠C的大小为
30°
30°
．
B（《坐标系与参数方程选讲》选做题）．已知直线的极坐标方程为ρsin(θ+
π
4
)=
2
2
，则点A（2，
7π
4
）到这条直线的距离为
2
2
2
2
．
C（不等式选讲）不等式|x-1|+|x|＜3的解集是
（-1，2）
（-1，2）
．
（2012•咸阳三模）（考生注意：请在下列三道试题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（不等式选做题）若不等式|2a-1|≤ |x+
1
x
|对一切非零实数x恒成立，则实数a的取值范围为
[-
1
2
，
3
2
]
[-
1
2
，
3
2
]
．
B．（几何证明选做题）如图，直角三角形ABC中，∠B=90°，AB=4，以BC为直径的圆交AC边于点D，AD=2，则∠C的大小为
30°
30°
．
C．（极坐标与参数方程选做题）若直线l的极坐标方程为ρcos(θ-
π
4
)=3
2
，圆C：
x=cosθ
y=sinθ
（θ为参数）上的点到直线l的距离为d，则d的最大值为
3
2
+1
3
2
+1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网