题目内容

直角三角形ABC中，斜边BC长为2，O是平面ABC内一点，点
-m
满足
OP
=
OA
+
1
2
(
AB
+
AC
)，则|
AP
|=
 
．
分析：把已知的等式进行等价变形得
AP
=
1
2
（
AB
+
AC
），求向量模可先求平方，最后利用直角三角形即可求出所求．
解答：解：∵动点P满足
OP
=
OA
+
1
2
(
AB
+
AC
)，
∴
AP
=
1
2
（
AB
+
AC
），
∴|
AP
|2=
1
4
（AB2+AC2+2
AB
•
AC
）=
1
4
（4+0）=1
故答案为：1．
点评：本题考查向量的加减运算，两个向量的数量积，体现了等价转化的数学思想，属于中档题．
练习册系列答案
相关题目
等腰直角三角形ABC中，AB=1，锐角顶点C在平面α内，β∥α，α、β的距离为1，随意旋转三角形ABC，则三角形ABC在β另一侧的最大面积为
 
．
15、（选做题）（几何证明选讲选做题）如图，直角三角形ABC中，∠B=90°，AB=4，以BC为直径的圆交AC边于点D，AD=2，则∠C的大小为
30°
．
（2012•宝鸡模拟）如图，已知PA⊥平面ABC，且PA=
2
，等腰直角三角形ABC中，AB=BC=1，AB⊥BC，AD⊥PB于D，AE⊥PC于E．
（1）求证：PC⊥平面ADE；
（2）求直线AB与平面ADE所成角的大小．
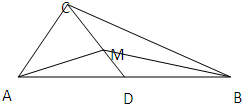精英家教网如图：直角三角形ABC中，AC⊥BC，AB=2，D是AB的中点，M是CD上的动点．
（1）若M是CD的中点，求
MA
•
MB
的值；
（2）求(
MA
+
MB
)•
MC
的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网