题目内容
15、（选做题）（几何证明选讲选做题）如图，直角三角形ABC中，∠B=90°，AB=4，以BC为直径的圆交AC边于点D，AD=2，则∠C的大小为30°
．分析：由圆的切线判定定理，结合已知中直角三角形ABC中，∠B=90°，以BC为直径的圆交AC边于点D，我们易得AB为圆的切线，则由切割线定理及AB=4，AD=2，我们易计算出斜边AC的长度，解直角三角形ABC，即可求出∠C的大小．
解答：解：∵∠B=90°，AB=4，BC为圆的直径
∴AB与圆相切，
由切割线定理得，
AB2=AD•AC
∴AC=8
故∠C=30°
故答案为：30°
∴AB与圆相切，
由切割线定理得，
AB2=AD•AC
∴AC=8
故∠C=30°
故答案为：30°
点评：本题考查的知识点是切线的判定及切割线定理，其中根据已知中直角三角形ABC中，∠B=90°，以BC为直径的圆交AC边于点D，判断出AB为圆的切线是解答本题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
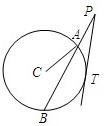（选做题）（几何证明选讲）如图所示，过圆C外一点P做一条直线与圆C交于A，B两点，BA=2AP，PT与圆C相切于T点．已知圆C的半径为2，∠CAB=30°，则PT=
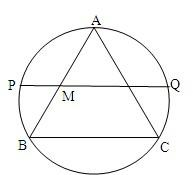（选做题）（几何证明选讲）如图，正△ABC的边长为2，点M，N分别是边AB，AC的中点，直线MN与△ABC的外接圆的交点为P、Q，则线段PM=
（附加题-选做题）（几何证明选讲）
的直径
，
为圆周上一点，
，过
作圆的切线
，过
作
的垂线
，
分别与直线
、圆交于点
、
，则 ∠
＝ ，线段
的长为 . 