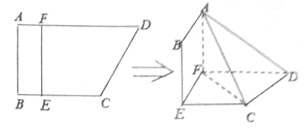
��Ŀ����
����Ŀ�����һ��ʵ������{an}���������� ![]() ��dΪ������n��N*���������һ���С�α�Ȳ����С���d��Ϊ��α������������й���ij��α�Ȳ�����{an}�Ľ��ۣ��ٶ������������a1 �� ��d��0������һ���б�Ϊ�������У��ڵ�d��0��a1��0ʱ����һ���б�Ϊ�����������У�����һ���п�����һ���������У�������һ���е�����Ϊ1��α����Ϊ3��-
��dΪ������n��N*���������һ���С�α�Ȳ����С���d��Ϊ��α������������й���ij��α�Ȳ�����{an}�Ľ��ۣ��ٶ������������a1 �� ��d��0������һ���б�Ϊ�������У��ڵ�d��0��a1��0ʱ����һ���б�Ϊ�����������У�����һ���п�����һ���������У�������һ���е�����Ϊ1��α����Ϊ3��- ![]() ��������һ�����е�һ�n��N*������һ���е�����Ϊ0��������Ϊ��1������һ���е�α���������
��������һ�����е�һ�n��N*������һ���е�����Ϊ0��������Ϊ��1������һ���е�α��������� ![]() ��������ȷ�Ľ����� ��
��������ȷ�Ľ����� ��
���𰸡��ۢ�
���������⣺�ٵ�a1= ![]() ��d=��
��d=�� ![]() ��an��0ʱ��
��an��0ʱ��
�����⣬an= ![]() ���ʲ���ȷ��
���ʲ���ȷ��
�ڵ�d��0��a1��0ʱ��
��an+1=�� ![]() ��
��
����һ���в��ǵ����������У��ʲ���ȷ��
����֪��α����d=0��an=1ʱ����һ�������������У�����ȷ��
�ܡ�a1=1��d=3��
��a2=�� ![]() =��2��
=��2��
�൱a2=2ʱa3=�� ![]()
![]() ������ȷ��
������ȷ��
�ݡ�a1=0��a3=��1��
�� ![]() =a1+d=d��
=a1+d=d��
��d��0��
�� ![]() ��0���ʲ���ȷ��
��0���ʲ���ȷ��
�����������ۢ���ȷ���٢ڢݲ���ȷ��
���Դ��ǣ��ۢܣ�
�����㾫����������Ҫ���������е�ͨ�ʽ�����֪ʶ�㣬��Ҫ�����������an�ĵ�n����n֮��Ĺ�ϵ������һ����ʽ��ʾ����ô�����ʽ�ͽ�������е�ͨ�ʽ������ȷ�����⣮

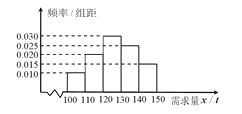
����Ŀ��ijѧУΪ����ȫ��ѧ��Ϊ����ѧ����������һԪǮ��һƬ�ģ�������ˮ�����ѧ���ڹ�ˮ��ÿ��ȡһƿ��Ȫˮ�����Ծ�������������Ͷ��һԪǮ����ͳ��������5����۳�����������������
�۳�ˮ��x����λ���䣩 | 7 | 6 | 6 | 5 | 6 |
����y����λ��Ԫ�� | 165 | 142 | 148 | 125 | 150 |
��1����y����x�����Իع鷽�̣�
��2��Ԥ���۳�8��ˮ�������Ƕ���Ԫ��
�����ع�ֱ�ߵ���С���˷����ƹ�ʽ�ֱ�Ϊ��![]() =
=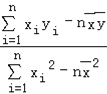 ��
��![]() =
=![]() ��
��![]()
![]() ��
��
����Ŀ��ij��ͬѧ���ù���ڽ������ʵ������[25��55]�����Ⱥ�����ȡ![]() �˽�����һ������ϰ���Ƿ���ϵ�̼����ĵ��飬������ϰ�߷��ϵ�̼����ij�Ϊ����̼�����������Ϊ���ǵ�̼�������õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�˽�����һ������ϰ���Ƿ���ϵ�̼����ĵ��飬������ϰ�߷��ϵ�̼����ij�Ϊ����̼�����������Ϊ���ǵ�̼�������õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
���� | ���� | ��̼������� | ռ�����Ƶ�� |
��һ�� | [25��30) | 120 | 0.6 |
�ڶ��� | [30��35) | 195 |
|
������ | [35��40) | 100 | 0.5 |
������ | [40��45) |
| 0.4 |
������ | [45��50) | 30 | 0.3 |
������ | [50��55] | 15 | 0.3 |
(1)��ȫƵ�ʷֲ�ֱ��ͼ����![]() ��ֵ��
��ֵ��
(2)���������[40��50)������̼�����в��÷ֲ��������ȡ6�˲μӻ����̼����������ѡȡ2����Ϊ��ӣ���ѡȡ��2�������ǡ��1��������[40��45)��ĸ���. 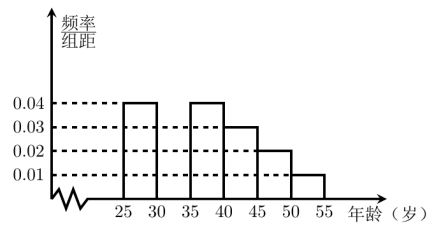
����Ŀ���ף�����̨����ͬʱ����һ�������������������ָ�껮�֣�ָ����ڻ����95Ϊ��Ʒ��С��95Ϊ��Ʒ���������ȡ����̨���������������100�����м�⣬�����ͳ�����£�
����ָ�� |
|
|
|
|
|
������ | 8 | 12 | 40 | 32 | 8 |
������ | 7 | 18 | 40 | 29 | 6 |
��1���Էֱ���Ƽ������һ������������Ϊ��Ʒ�ĸ��ʣ�
��2����������һ�������������Ʒ��ӯ��160Ԫ����Ʒ�����20Ԫ���һ�������һ�������������Ʒ��ӯ��200Ԫ����Ʒ�����40Ԫ���ڣ�1����ǰ���£����������������2�����Ի�����������ֵΪ�������ݣ�Ӧ����ΰ���������ѣ�