Question

【题目】已知函数f（x）=4cosxsin（x+ ）﹣1， （Ⅰ）求f（x）的单调递增区间
（Ⅱ）若sin2x+af（x+ ）+1＞6cos4x对任意x∈（﹣ ， ）恒成立，求实数a的取值范围．

Answer 1

【答案】解：（Ⅰ）由函数f（x）=4cosxsin（x+ ）﹣1，

可得：f（x）=4cosx（ sinx+ cosx）﹣1

= sin2x+2cos2x﹣1

= sin2x+cos2x

=2sin（2x+ ）

由 （k∈Z），

解得：

所以：f（x）的单调增区间为

（Ⅱ）由题意：当 时，

原不等式等价于a2cos2x＞6cos4x﹣sin2x﹣1，

即 恒成立

令 =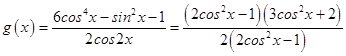

∵ ，当x=0时，cosx取得最大值，即cosx=1时，那么g（x）也取得最大值为 ．

因此， ．

【解析】（Ⅰ）先利用两角和余差的基本公式和辅助角公式将函数化为y=Asin（ωx+φ）的形式，再将内层函数看作整体，放到正弦函数的增区间上，解不等式得函数的单调递增区间；

（Ⅱ）求出f（x+ ）的值，带到题设中去，化简，求函数在x∈（﹣ ， ）的最值，即可恒成立，从而求实数a的取值范围．

【考点精析】利用正弦函数的单调性和三角函数的最值对题目进行判断即可得到答案，需要熟知正弦函数的单调性：在上是增函数；在上是减函数；函数，当时，取得最小值为；当时，取得最大值为，则，，．