Question

【题目】已知函数 （a＞0，a≠1）．
（1）判断函数f（x）的奇偶性；
（2）判断函数f（x）在（1，+∞）上的单调性，并给出证明；
（3）当x∈（n，a﹣2）时，函数f（x）的值域是（1，+∞），求实数a与n的值．

Answer 1

【答案】
（1）解：由 得函数f（x）的定义域为（1，+∞）∪（﹣∞，﹣1），

又

所以f（x）为奇函数

（2）解：由（1）及题设知： ，设 ，

∴当x1＞x2＞1时， ∴t1＜t2．

当a＞1时，logat1＜logat2，即f（x1）＜f（x2）．

∴当a＞1时，f（x）在（1，+∞）上是减函数．

同理当0＜a＜1时，f（x）在（1，+∞）上是增函数

（3）解：①当n＜a﹣2≤﹣1时，有0＜a＜1．

由（2）可知：f（x）在（n，a﹣2）为增函数，

由其值域为（1，+∞）知 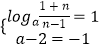，无解

②当1≤n＜a﹣2时，有a＞3．由（2）知：f（x）在（n，a﹣2）为减函数，

由其值域为（1，+∞）知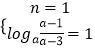

得 ，n=1

【解析】（1）先求函数的定义域看是否关于原点对称，然后在用奇偶函数的定义判断，要注意到代入﹣x时，真数是原来的倒数，这样就不难并判断奇偶性．（2）用单调性的定义进行证明，首先在所给的区间上任取两个自变量看真数的大小关系，然后在根据底的不同判断函数单调性．（3）要根据第二问的结论，进行分类讨论，解出两种情况下的实数a与n的值．