题目内容
17．若（2x-$\frac{1}{x}$）n的展开式中仅第4项的二项式系数最大，则它的第四项系数是-160．分析 利用二项式系数的性质：展开式中中间项的二项式系数最大求出n；利用二项展开式的通项公式求出第4项的系数．
解答 解：∵展开式中中间项的二项式系数最大，
∴展开式共7项，
∴n=6．
∴第4项的系数是-${C}_{6}^{3}•{2}^{3}$=-160．
故答案为：-160．
点评 本题考查二项式系数的性质：中间项的二项式系数最大、考查利用二项展开式的通项公式解决二项展开式的特定项问题．
练习册系列答案
相关题目
8．
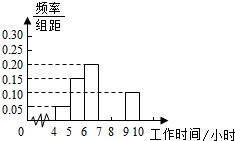某高新区一工厂为了了解工人的工作时间（单位：小时），从该工厂抽取20名工人的工作时间作为样本进行调查，调查的数据分组整理后如表所示，并作出样本的部分频率分布直方图如图．
（1）求表中a，b，x的值，并补齐频率分布直方图；
（2）现从工作时间在[4，5]和[6，7）内的工人中随机抽取2名，求抽到的2名工人的工作时间都在[6，7）内的概率．
某高新区一工厂为了了解工人的工作时间（单位：小时），从该工厂抽取20名工人的工作时间作为样本进行调查，调查的数据分组整理后如表所示，并作出样本的部分频率分布直方图如图．| 工作时间（小时） | [4，5） | [5，6） | [6，7） | [7，8） | [8，9） | [9，10） |
| 频数 | 1 | 3 | 4 | a | b | 2 |
| 频率 | 0.05 | 0.15 | 0.20 | 0.30 | x | 0.10 |
（2）现从工作时间在[4，5]和[6，7）内的工人中随机抽取2名，求抽到的2名工人的工作时间都在[6，7）内的概率．
7．
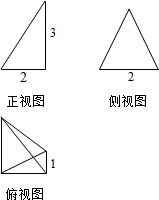一个几何体的三视图如图所示，则该几何体的体积为（ ）
一个几何体的三视图如图所示，则该几何体的体积为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |