题目内容
已知数列{an}的通项公式是an=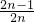 ,其前n项和Sn=
,其前n项和Sn= ,则项数n等于
,则项数n等于
- A.13
- B.10
- C.9
- D.6
D
分析:先将数列的通项变形,再求和,利用已知条件建立方程,即可求得数列的项数n
解答:∵数列{an}的通项公式是an=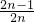 ,
,
∴an=1-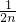 ,
,
∴Sn=(1- )+(1-
)+(1- )+(1-
)+(1- )+…+(1-
)+…+(1-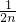 )
)
=n-( +
+ +
+ +…+
+…+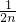 )
)
=n-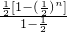 =n-1+
=n-1+ .
.
由Sn= =n-1+
=n-1+ ,
,
∴可得出n=6.
故选D
点评:本题考查了数列的通项,考查数列的求和,解题时掌握公式是关键,属于基础题.
分析:先将数列的通项变形,再求和,利用已知条件建立方程,即可求得数列的项数n
解答:∵数列{an}的通项公式是an=
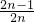 ,
,∴an=1-
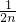 ,
,∴Sn=(1-
 )+(1-
)+(1- )+(1-
)+(1- )+…+(1-
)+…+(1-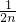 )
)=n-(
 +
+ +
+ +…+
+…+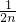 )
)=n-
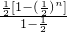 =n-1+
=n-1+ .
.由Sn=
 =n-1+
=n-1+ ,
,∴可得出n=6.
故选D
点评:本题考查了数列的通项,考查数列的求和,解题时掌握公式是关键,属于基础题.

练习册系列答案
相关题目
已知数列{an}的通项为an=2n-1,Sn为数列{an}的前n项和,令bn=
,则数列{bn}的前n项和的取值范围为( )
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|