题目内容
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的普通方程为
的普通方程为![]() .在以坐标原点为极点,
.在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出圆![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点Q在
上,点Q在![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
【答案】(1)圆![]() 的参数方程:
的参数方程: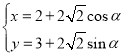 ,直线
,直线![]() :
:![]() ;(2)
;(2)![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()
【解析】
(1)整理圆![]() 的方程为
的方程为![]() ,即可写出参数方程,利用
,即可写出参数方程,利用![]() 将直线方程写为直角坐标方程即可;
将直线方程写为直角坐标方程即可;
(2)法一:利用参数方程设曲线![]() 上的点
上的点![]() ,利用点到直线距离公式可得
,利用点到直线距离公式可得![]() ,则根据三角函数的性质求处最值,并将
,则根据三角函数的性质求处最值,并将![]() 代回求得坐标;
代回求得坐标;
法二:![]() 为圆心到直线距离减去半径,再利用弦与直线垂直的性质得
为圆心到直线距离减去半径,再利用弦与直线垂直的性质得![]() 所在直线为
所在直线为![]() ,联立直线与圆的方程即可求得交点
,联立直线与圆的方程即可求得交点![]() 的坐标
的坐标
(1)圆![]() 的方程可化为
的方程可化为![]() ,圆心为
,圆心为![]() ,半径为
,半径为![]() ,
,
∴圆![]() 的参数方程为
的参数方程为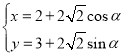 (
(![]() 为参数),
为参数),
直线![]() 的极坐标方程可化为
的极坐标方程可化为![]() ,
,
∵![]() ,∴直线
,∴直线![]() 的直角坐标方程为
的直角坐标方程为![]()
(2)法一:设曲线![]() 上的点
上的点![]() ,
,
点![]() 到直线
到直线![]() :
:![]() 的距离:
的距离:
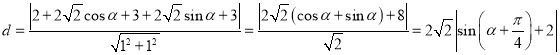 ,
,
当![]() 时,
时,![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ,所以
,所以![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()
法二:曲线![]() 是以
是以![]() 为圆心,半径为
为圆心,半径为![]() 的圆,
的圆,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() ,
,
此时直线![]() 经过圆心
经过圆心![]() ,且与直线
,且与直线![]() 垂直,
垂直,
![]() ,所以
,所以![]() ,
,![]() 所在直线方程为
所在直线方程为![]() ,即
,即![]() ,
,
联立直线和圆的方程![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 取得最小值时,点
取得最小值时,点![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某种零件的质量指标值为整数,指标值为8时称为合格品,指标值为7或者9时称为准合格品,指标值为6或10时称为废品,某单位拥有一台制造该零件的机器,为了了解机器性能,随机抽取了该机器制造的100个零件,不同的质量指标值对应的零件个数如下表所示;
质量指标值 | 6 | 7 | 8 | 9 | 10 |
零件个数 | 6 | 18 | 60 | 12 | 4 |
使用该机器制造的一个零件成本为5元,合格品可以以每个![]() 元的价格出售给批发商,准合格品与废品无法岀售.
元的价格出售给批发商,准合格品与废品无法岀售.
(1)估计该机器制造零件的质量指标值的平均数;
(2)若该单位接到一张订单,需要该零件2100个,为使此次交易获利达到1400元,估计![]() 的最小值;
的最小值;
(3)该单位引进了一台加工设备,每个零件花费2元可以被加工一次,加工结果会等可能出现以下三种情况:①质量指标值增加1,②质量指标值不变,③质量指标值减少1.已知每个零件最多可被加工一次,且该单位计划将所有准合格品逐一加工,在(2)的条件下,估计![]() 的最小值(精确到0.01) .
的最小值(精确到0.01) .