Question

【题目】在直角坐标系xOy中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系；曲线C1的普通方程为(x-1)2 +y2 =1，曲线C2的参数方程为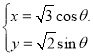（θ为参数）.

（Ⅰ）求曲线C1和C2的极坐标方程：

（Ⅱ）设射线θ=(ρ>0)分别与曲线C1和C2相交于A，B两点，求|AB|的值．

Answer 1

【答案】（Ⅰ），;（Ⅱ）

【解析】

（Ⅰ）根据，可得曲线C1的极坐标方程，然后先计算曲线C2的普通方程，最后根据极坐标与直角坐标的转化公式，可得结果.

（Ⅱ）将射线θ=分别与曲线C1和C2极坐标方程联立，可得A，B的极坐标，然后简单计算，可得结果.

（Ⅰ）

由

所以曲线的极坐标方程为，

曲线的普通方程为

则曲线的极坐标方程为

（Ⅱ）令，则，，

则，即，

所以，，

故．