题目内容
【题目】已知等差数列![]() 的公差不为零,且
的公差不为零,且![]() ,
,![]() 、
、![]() 、
、![]() 成等比数列,数列
成等比数列,数列![]() 满足
满足![]()
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)求证: .
.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)设等差数列![]() 的公差为
的公差为![]() ,
,![]() ,运用等差数列的通项公式和等比数列的中项性质,解方程可得首项和公差,进而得到
,运用等差数列的通项公式和等比数列的中项性质,解方程可得首项和公差,进而得到![]() ,可令
,可令![]() ,求得
,求得![]() ,再将
,再将![]() 换为
换为![]() ,相减可得
,相减可得![]() ;
;
(2)原不等式转化为![]() ,应用数学归纳法证明,注意检验
,应用数学归纳法证明,注意检验![]() 时不等式成立,再假设
时不等式成立,再假设![]() 时不等式成立,证明
时不等式成立,证明![]() 时,不等式也成立,注意运用分析法证明.
时,不等式也成立,注意运用分析法证明.
(1)等差数列![]() 的公差
的公差![]() 不为零,
不为零,![]() ,可得
,可得![]() ,
,
![]() 、
、![]() 、
、![]() 成等比数列,可得
成等比数列,可得![]() ,即
,即![]() ,
,
解方程可得![]() ,则
,则![]() .
.
数列![]() 满足
满足![]() ,可得
,可得![]() ,
,
当![]() 时,由
时,由![]() ,
,
可得![]() ,
,
相减可得![]() ,则
,则![]() ,
,![]() 也适合
也适合![]() ,则
,则![]() ,
,![]() ;
;
(2)证明:不等式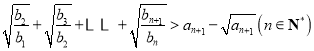 即为
即为
![]() ,
,
下面应用数学归纳法证明.
(i)当![]() 时,不等式的左边为
时,不等式的左边为![]() ,右边为
,右边为![]() ,左边
,左边![]() 右边,不等式成立;
右边,不等式成立;
(ii)假设![]() 时,不等式
时,不等式![]() 成立,
成立,
当![]() 时,
时,![]() ,
,
要证![]() ,
,
只要证![]() ,
,
即证![]() ,
,
即证![]() ,
,
由![]() ,可得上式成立,可得
,可得上式成立,可得![]() 时,不等式也成立.
时,不等式也成立.
综上可得,对一切![]() ,
,![]() ,
,
故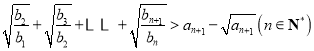 .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目