题目内容
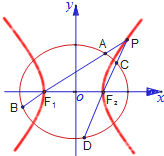 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线PF1、PF2的斜率分别为k1、k2,证明k1•k2=1;
(Ⅲ)(此小题仅理科做)是否存在常数λ,使得|AB|+|CD|=λ|AB|•|CD|恒成立?若存在,求λ的值;若不存在,请说明理由.
分析:(Ⅰ)由题意知,椭圆离心率为
=
,及椭圆的定义得到又2a+2c=4(
+1),解方程组即可求得椭圆的方程,等轴双曲线的顶点是该椭圆的焦点可求得该双曲线的方程;
(Ⅱ)设点P(x0,y0),根据斜率公式求得k1、k2,把点P(x0,y0)在双曲线上,即可证明结果;
(Ⅲ)设直线AB的方程为y=k(x+2),则可求出直线CD的方程为y=
(x-2),联立直线和椭圆方程,利用韦达定理,即可求得|AB|,|CD|,代入|AB|+|CD|=λ|AB|•|CD|,求得λ的值.
| c |
| a |
| ||
| 2 |
| 2 |
(Ⅱ)设点P(x0,y0),根据斜率公式求得k1、k2,把点P(x0,y0)在双曲线上,即可证明结果;
(Ⅲ)设直线AB的方程为y=k(x+2),则可求出直线CD的方程为y=
| 1 |
| k |
解答:解:(Ⅰ)由题意知,椭圆离心率为
=
,
得a=
c,又2a+2c=4(
+1),
所以可解得a=2
,c=2,所以b2=a2-c2=4,
所以椭圆的标准方程为
+
=1;
所以椭圆的焦点坐标为(±2,0),
因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,
所以该双曲线的标准方程为
-
=1.
(Ⅱ)设点P(x0,y0),
则k1=
,k2=
,
∴k1•k2=
=
,
又点P(x0,y0)在双曲线上,
∴
-
=1,即y02=x02-4,
∴k1•k2=
=1.
(Ⅲ)假设存在常数λ,使得得|AB|+|CD|=λ|AB|•|CD|恒成立,
则由(II)知k1•k2=1,
∴设直线AB的方程为y=k(x+2),则直线CD的方程为y=
(x-2),
由方程组
消y得:(2k2+1)x2+8k2x+8k2-8=0,
设A(x1,y1),B(x2,y2),
则由韦达定理得,x1+x2=
,x1•x2=
,
∴AB=
=
,
同理可得CD=
=
=
,
∵|AB|+|CD|=λ|AB|•|CD|,
∴λ=
+
=
-
=
=
,
∴存在常数λ=
,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
| c |
| a |
| ||
| 2 |
得a=
| 2 |
| 2 |
所以可解得a=2
| 2 |
所以椭圆的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
所以椭圆的焦点坐标为(±2,0),
因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,
所以该双曲线的标准方程为
| x2 |
| 4 |
| y2 |
| 4 |
(Ⅱ)设点P(x0,y0),
则k1=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
∴k1•k2=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
| y02 |
| x02-4 |
又点P(x0,y0)在双曲线上,
∴
| x02 |
| 4 |
| y02 |
| 4 |
∴k1•k2=
| y02 |
| x02-4 |
(Ⅲ)假设存在常数λ,使得得|AB|+|CD|=λ|AB|•|CD|恒成立,
则由(II)知k1•k2=1,
∴设直线AB的方程为y=k(x+2),则直线CD的方程为y=
| 1 |
| k |
由方程组
|
设A(x1,y1),B(x2,y2),
则由韦达定理得,x1+x2=
| -8k2 |
| 1+2k2 |
| 8k2-8 |
| 2k2+1 |
∴AB=
| 1+k2 |
| (x1+x2)2-4x1 x2 |
4
| ||
| 2k2+1 |
同理可得CD=
1+(
|
| (x1+x2)2-4x1x2 |
4
| ||||
2
|
4
| ||
| k2+2 |
∵|AB|+|CD|=λ|AB|•|CD|,
∴λ=
| 1 |
| |AB| |
| 1 |
| |CD| |
4
| ||
| 2k2+1 |
4
| ||
| k2+2 |
| 3+3k2 | ||
4
|
3
| ||
| 8 |
∴存在常数λ=
3
| ||
| 8 |
点评:本题考查了椭圆的定义、离心率、椭圆与双曲线的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.其中问题(III)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
相关题目
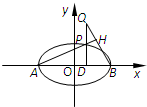 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆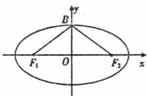 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆