题目内容
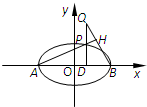 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 3 |
| PQ |
| QD |
(1)试求椭圆的标准方程;
(2)P在C处时,若∠QAB=2∠PAB,试求过Q、A、D三点的圆的方程;
(3)若直线QB与AP交于点H,问是否存在λ,使得线段OH的长为定值,若存在,求出λ的值;若不存在,说明理由.
分析:(1)把点C代入椭圆方程可得a,b的一个方程,由离心率为
,得
=
,再结合a2=b2+c2可得a,b;
(2)易知所求圆的直径为AQ,通过解直角三角形可求tan∠PAB,由二倍角的正切公式可求tan∠QAB,从而可得Q点的坐标,进而可得圆心、半径;
(3)设P(x0,y0),H(x,y),由H、A、P三点共线及Q、H、B三点共线可得x,y的方程组,解出x,y,用x0,λ表示出OH2,根据其为定值可得方程,解出即可;
| ||
| 3 |
| c |
| a |
| ||
| 3 |
(2)易知所求圆的直径为AQ,通过解直角三角形可求tan∠PAB,由二倍角的正切公式可求tan∠QAB,从而可得Q点的坐标,进而可得圆心、半径;
(3)设P(x0,y0),H(x,y),由H、A、P三点共线及Q、H、B三点共线可得x,y的方程组,解出x,y,用x0,λ表示出OH2,根据其为定值可得方程,解出即可;
解答:解:(1)由椭圆过点C,得
+
=1,即
+
=1①,
由离心率为
,得
=
,所以
=
=
,得a2=3b2②,
联立①②解得a2=3,b2=1,
所以椭圆的标准方程为:
+y2=1;
(2)由(1)得A(-
,0),
当P在C处时,D(
,0),P(
,
),
tan∠PAB=
=
=
,
则tan∠QAB=
=
=
,则
=
,QD=
×
=
,
所以Q(
,
),易知过Q、A、D三点的圆以AQ为直径,则圆心为(-
,
),直径AQ=
=
,
半径为
,
故所求圆的方程为(x+
)2+(y-
)2=
;
(3)存在λ=-
满足条件,理由如下:
设P(x0,y0),则D(x0,0),由
=λ
,得(0,yQ-y0)=λ(0,-yQ),可得yQ=
,则Q(x0,
),
设H(x,y),由H、A、P三点共线,得kAH=kAP,即
=
①,同理由Q、H、B三点共线可得
=
②,
联立①②解得
,又点P在椭圆上,所以
+y02=1,
所以OH2=x2+y2=[
]2+[
]2
=[
]2+
=
,
若线段OH的长为定值,须有
=
=
,
解得λ=-
,
故存在满足条件的λ=-
.
(
| ||||
| a2 |
(
| ||||
| b2 |
| 3 |
| 4a2 |
| 3 |
| 4b2 |
由离心率为
| ||
| 3 |
| c |
| a |
| ||
| 3 |
| c2 |
| a2 |
| a2-b2 |
| a2 |
| 2 |
| 3 |
联立①②解得a2=3,b2=1,
所以椭圆的标准方程为:
| x2 |
| 3 |
(2)由(1)得A(-
| 3 |
当P在C处时,D(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
tan∠PAB=
| PD |
| AD |
| ||||||
|
| 1 |
| 3 |
则tan∠QAB=
| 2tan∠PAB |
| 1-tan2∠PAB |
2×
| ||
1-(
|
| 3 |
| 4 |
| QD |
| AD |
| 3 |
| 4 |
| 3 |
| 4 |
3
| ||
| 2 |
9
| ||
| 8 |
所以Q(
| ||
| 2 |
9
| ||
| 8 |
| ||
| 4 |
9
| ||
| 16 |
(
|
15
| ||
| 8 |
半径为
15
| ||
| 16 |
故所求圆的方程为(x+
| ||
| 4 |
9
| ||
| 16 |
| 675 |
| 256 |
(3)存在λ=-
| 2 |
| 3 |
设P(x0,y0),则D(x0,0),由
| PQ |
| QD |
| y0 |
| 1+λ |
| y0 |
| 1+λ |
设H(x,y),由H、A、P三点共线,得kAH=kAP,即
| y | ||
x+
|
| y0 | ||
x0+
|
| y | ||
x-
|
| y0 | ||
(1+λ)(x0-
|
联立①②解得
|
| x02 |
| 3 |
所以OH2=x2+y2=[
(2
| ||||
2
|
2
| ||||
2
|
=[
(2
| ||||
2
|
12(1-
| ||||
[2
|
=
(8+12λ+3λ2)x02-6
| ||||
λ2x02-(4
|
若线段OH的长为定值,须有
| 8+12λ+3λ2 |
| λ2 |
-6
| ||||
-(4
|
| 9λ2+12 |
| 3λ2+12λ |
解得λ=-
| 2 |
| 3 |
故存在满足条件的λ=-
| 2 |
| 3 |
点评:本题考查椭圆的标准方程、直线与椭圆的位置关系,考查学生综合运用知识分析问题解决问题的能力,本题综合性强、运算量大,对能力要求很高.

练习册系列答案
相关题目
 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆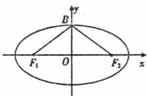 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆