题目内容
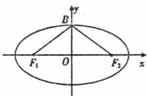 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
(1)求椭圆的方程;
(2)是否存在这样的直线使得直线l与椭圆交于M,N两点,且椭圆右焦点F2恰为△BMN的垂心?若存在,求出直线l的方程;若不存在,请说明由..
分析:(1)根据椭圆
+
=1(a>b>0)的离心率为
,可得
=
,利用△BF1F2的周长为4+2
,可得a+c=2+
,由此可求椭圆的方程;
(2)假设存在直线使得直线l与椭圆交于M,N两点,且椭圆右焦点F2恰为△BMN的垂心,设M(x1,y1),N(x2,y2),确定kMN=
设l的方程为y=
x+m,代入
+y2=1,利用
=(x1-
,y1),
=(x2,y2-1),
⊥
,即可求得满足条件的直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| 3 |
| 3 |
(2)假设存在直线使得直线l与椭圆交于M,N两点,且椭圆右焦点F2恰为△BMN的垂心,设M(x1,y1),N(x2,y2),确定kMN=
| 3 |
| 3 |
| x2 |
| 4 |
| F2M |
| 3 |
| BN |
| F2M |
| BN |
解答:解:(1)∵椭圆
+
=1(a>b>0)的离心率为
,∴
=
①
∵△BF1F2的周长为4+2
,∴a+c=2+
②
由①②可得c=
,a=2,∴b=
=1
∴椭圆的方程为
+y2=1;
(2)假设存在直线使得直线l与椭圆交于M,N两点,且椭圆右焦点F2恰为△BMN的垂心
设M(x1,y1),N(x2,y2),∵B(0,1),F2(
,0),∴kMF2=-
,∴kMN=
设l的方程为y=
x+m,代入
+y2=1消元可得13x2+8
mx+4(m2-1)=0
∴x1+x2=-
,x1x2=
③
∵
=(x1-
,y1),
=(x2,y2-1),
⊥
∴
•
=x2(x1-
)+y1(y2-1)=4x1x2+
(m-1)(x1+x2) +m(m-1)=0④
③代入④,可得4×
-
(m-1)×
+m(m-1)=0
∴(m-1)(5m+16)=0
∴m=1,或m=-
经检验,当m=1时直线l经过点B,不能构成三角形,故舍去
∴存在直线l:y=
x-
满足条件.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
∵△BF1F2的周长为4+2
| 3 |
| 3 |
由①②可得c=
| 3 |
| a2-c2 |
∴椭圆的方程为
| x2 |
| 4 |
(2)假设存在直线使得直线l与椭圆交于M,N两点,且椭圆右焦点F2恰为△BMN的垂心
设M(x1,y1),N(x2,y2),∵B(0,1),F2(
| 3 |
| ||
| 3 |
| 3 |
设l的方程为y=
| 3 |
| x2 |
| 4 |
| 3 |
∴x1+x2=-
8
| ||
| 13 |
| 4(m2-1) |
| 13 |
∵
| F2M |
| 3 |
| BN |
| F2M |
| BN |
∴
| F2M |
| BN |
| 3 |
| 3 |
③代入④,可得4×
| 4(m2-1) |
| 13 |
| 3 |
8
| ||
| 13 |
∴(m-1)(5m+16)=0
∴m=1,或m=-
| 16 |
| 5 |
经检验,当m=1时直线l经过点B,不能构成三角形,故舍去
∴存在直线l:y=
| 3 |
| 16 |
| 3 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,联立方程,利用数量积为0是解题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目