题目内容
已知正三棱锥P—ABC的各棱长都为2，底面为ABC，棱PC的中点为M，从A点出发，在三棱锥P—ABC的表面运动，经过棱PB到达点M的最短路径之长为
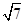
解：正三棱锥P—ABC的各棱长都为2，底面为ABC，棱PC的中点为M，从A点出发，在三棱锥P—ABC的表面运动，经过棱PB到达点M的最短路径就是得到展开图，利用两点距离得到最小值为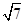
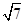
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
孟建平小学滚动测试系列答案黄冈天天练口算题卡系列答案
中，底面
是直角梯形，
∥
，
平面
，点
是
的中点，且
.
∥平面
；
，
，
AA′=1，点M，N分别为
和
的中点。
∥平面
；
的体积。（锥体体积公式V=
Sh,其中S为底面面积，h为高）
，则球的体积是_________.
，
，BC⊥CD .