题目内容
已知两点A(–2,0),B(0,2),点P是椭圆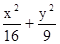 =1上任意一点,则点P到直线AB距离的最大值是______________.
=1上任意一点,则点P到直线AB距离的最大值是______________.
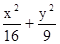 =1上任意一点,则点P到直线AB距离的最大值是______________.
=1上任意一点,则点P到直线AB距离的最大值是______________.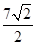
试题分析:本题最简捷的方法是用三角换元法求解.由于点P是椭圆
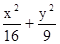 =1上任意一点,故可设P点坐标为
=1上任意一点,故可设P点坐标为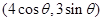 ,直线AB的方程为
,直线AB的方程为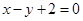 ,则P到直线AB的距离为
,则P到直线AB的距离为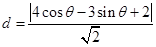
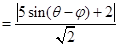 (其中
(其中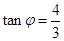 ,且
,且 为锐角),可见当
为锐角),可见当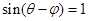 时,
时,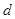 取得最大值
取得最大值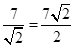 .
.
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
题目内容
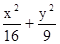 =1上任意一点,则点P到直线AB距离的最大值是______________.
=1上任意一点,则点P到直线AB距离的最大值是______________.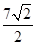
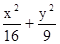 =1上任意一点,故可设P点坐标为
=1上任意一点,故可设P点坐标为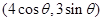 ,直线AB的方程为
,直线AB的方程为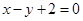 ,则P到直线AB的距离为
,则P到直线AB的距离为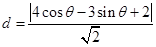
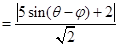 (其中
(其中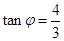 ,且
,且 为锐角),可见当
为锐角),可见当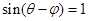 时,
时,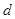 取得最大值
取得最大值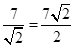 .
.
 同步轻松练习系列答案
同步轻松练习系列答案